Page 91 - Mechanics of Asphalt Microstructure and Micromechanics

84 Ch a p t e r Th r e e

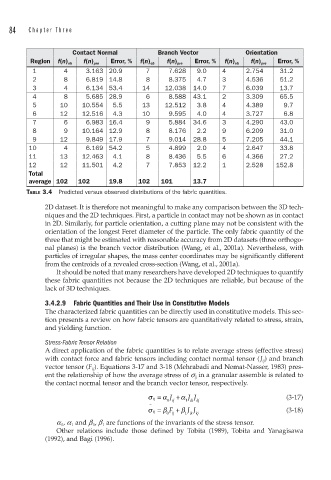
Contact Normal Branch Vector Orientation
Region f(n) ob f(n) pre Error, % f(n) ob f(n) pre Error, % f(n) ob f(n) pre Error, %
1 4 3.163 20.9 7 7.628 9.0 4 2.754 31.2
2 8 6.819 14.8 8 8.375 4.7 3 4.536 51.2
3 4 6.134 53.4 14 12.038 14.0 7 6.039 13.7
4 8 5.685 28.9 6 8.588 43.1 2 3.309 65.5
5 10 10.554 5.5 13 12.512 3.8 4 4.389 9.7
6 12 12.516 4.3 10 9.595 4.0 4 3.727 6.8
7 6 6.983 16.4 9 5.884 34.6 3 4.290 43.0
8 9 10.164 12.9 8 8.176 2.2 9 6.209 31.0
9 12 9.849 17.9 7 9.014 28.8 5 7.205 44.1
10 4 6.169 54.2 5 4.899 2.0 4 2.647 33.8
11 13 12.463 4.1 8 8.436 5.5 6 4.366 27.2
12 12 11.501 4.2 7 7.853 12.2 1 2.528 152.8
Total
average 102 102 19.8 102 101 13.7
TABLE 3.4 Predicted versus observed distributions of the fabric quantities.

2D dataset. It is therefore not meaningful to make any comparison between the 3D tech-
niques and the 2D techniques. First, a particle in contact may not be shown as in contact
in 2D. Similarly, for particle orientation, a cutting plane may not be consistent with the
orientation of the longest Feret diameter of the particle. The only fabric quantity of the
three that might be estimated with reasonable accuracy from 2D datasets (three orthogo-
nal planes) is the branch vector distribution (Wang, et al., 2001a). Nevertheless, with
particles of irregular shapes, the mass center coordinates may be significantly different
from the centroids of a revealed cross-section (Wang, et al., 2001a).
It should be noted that many researchers have developed 2D techniques to quantify
these fabric quantities not because the 2D techniques are reliable, but because of the
lack of 3D techniques.

3.4.2.9 Fabric Quantities and Their Use in Constitutive Models
The characterized fabric quantities can be directly used in constitutive models. This sec-
tion presents a review on how fabric tensors are quantitatively related to stress, strain,
and yielding function.

Stress-Fabric Tensor Relation
A direct application of the fabric quantities is to relate average stress (effective stress)
with contact force and fabric tensors including contact normal tensor (J ij ) and branch
vector tensor (F ij ). Equations 3-17 and 3-18 (Mehrabadi and Nemat-Nasser, 1983) pres-
ent the relationship of how the average stress of s ij in a granular assemble is related to
the contact normal tensor and the branch vector tensor, respectively.
−
σ = α J + α J J (3-17)
ij
− 0 ij 1 ik kj
σ = β F + β J J (3-18)
ij
0 ij 1 ik kj
a 0 , a 1 and b 0 , b 1 are functions of the invariants of the stress tensor.
Other relations include those defined by Tobita (1989), Tobita and Yanagisawa
(1992), and Bagi (1996).