Page 46 - Mechanics of Microelectromechanical Systems

1. Stiffness basics 33
as shown in Young and Budynas [4] or Lobontiu [8].

Example 1.8
Evaluate the relative difference (error) between the torsional stiffness of
a fixed-free, constant rectangular cross-section microbar when considered
very thin (t << w) versus the same stiffness when the cross-sectional
dimensions are simply related as t < w.

Solution:
As previously indicated, the torsion stiffness is proportional to the
torsion moment of inertia. As a consequence, differences between the
stiffness produced by the two models only arise from differences in the
respective moments of inertia. If the inertia moment of Eq. (1.118), which
corresponds to very thin bars, is denoted by and the one corresponding to
thin bars, Eq. (1.119), is the relative difference between the two moments
of inertia is:

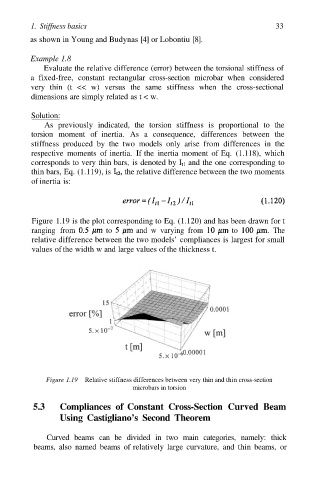
Figure 1.19 is the plot corresponding to Eq. (1.120) and has been drawn for t
ranging from to and w varying from to The
relative difference between the two models’ compliances is largest for small
values of the width w and large values of the thickness t.

Figure 1.19 Relative stiffness differences between very thin and thin cross-section
microbars in torsion

5.3 Compliances of Constant Cross-Section Curved Beam
Using Castigliano’s Second Theorem

Curved beams can be divided in two main categories, namely: thick
beams, also named beams of relatively large curvature, and thin beams, or