Page 254 - Microsensors, MEMS and Smart Devices - Gardner Varadhan and Awadelkarim

234 MICROSENSORS

200 300 400 500 600
Temperature, T(°K)
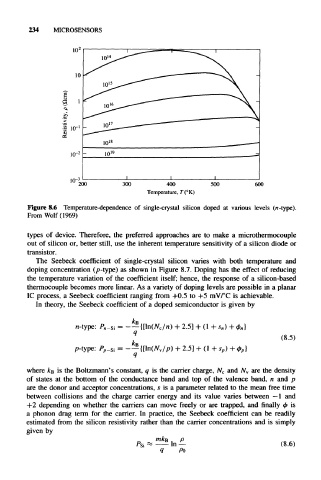
Figure 8.6 Temperature-dependence of single-crystal silicon doped at various levels (n-type).
From Wolf (1969)

types of device. Therefore, the preferred approaches are to make a microthermocouple
out of silicon or, better still, use the inherent temperature sensitivity of a silicon diode or
transistor.
The Seebeck coefficient of single-crystal silicon varies with both temperature and
doping concentration (p-type) as shown in Figure 8.7. Doping has the effect of reducing
the temperature variation of the coefficient itself; hence, the response of a silicon-based
thermocouple becomes more linear. As a variety of doping levels are possible in a planar
IC process, a Seebeck coefficient ranging from +0.5 to +5 mV/°C is achievable.
In theory, the Seebeck coefficient of a doped semiconductor is given by

n-type: />„_* = - — {[ln(N c/n) + 2.5] + (1 + 5,) + $„
q
(8.5)
p-type: P p_ Si = ~{[\n(N v/p) + 2.5] s p) + <t> p}

where k B is the Boltzmann's constant, q is the carrier charge, N c and N v are the density
of states at the bottom of the conductance band and top of the valence band, n and p
are the donor and acceptor concentrations, s is a parameter related to the mean free time
between collisions and the charge carrier energy and its value varies between —1 and
+2 depending on whether the carriers can move freely or are trapped, and finally <j> is
a phonon drag term for the carrier. In practice, the Seebeck coefficient can be readily
estimated from the silicon resistivity rather than the carrier concentrations and is simply
given by
p
In — (8.6)
PQ