Page 228 - Microtectonics

218 7 · Porphyroblasts and Reaction Rims

Box 7.4 Rotation or non-rotation of spiral-S porphyroblasts
i
Discussions by several authors have shown that it is difficult to S i spirals that can be interpreted as included strain shadows
find reliable criteria to determine if spiral-S i or oblique-S i por- are present (Figs. 7.33, 7.37a; Schoneveld 1977, 1979).
phyroblasts rotated with respect to kinematic axes of bulk flow the relative rotation angle of the porphyroblast exceeds 180°.
(as in Fig. 7.34b), or not (as in Fig. 7.34c,d,e) (e.g. Bell 1985; Bell in elongate crystals, the symmetry axis of the S i -spiral in the
and Johnson 1989; Bell et al. 1992; Passchier et al. 1992; Johnson crystals is parallel to the long axis, even in sets of porphyro-
1993a,b, 1999). Below we list some criteria that might be of help. blasts with variable orientation of the long axis (Busa and Gray
1992).
A rotational interpretation is likely to be correct if
An interpretation of a spiral- or oblique-S i inclusion pattern as the
the sense of rotation of the porphyroblast is confirmed by result of matrix deformation around a stable porphyroblast is prob-
other sense of shear markers (Busa and Gray 1992; Fig. 7.35). able if
S spirals in three dimensions have gradually decreasing ampli-
i
tude towards the rim of the crystal in both directions from the evidence is present that the foliation in the matrix has passed
core of the crystal along the symmetry axis of the spiral (Figs. 7.36b, trough folding and transposition (e.g. Fig. 7.34e).
7.37b; Powell and Treagus 1969, 1970; Busa and Gray 1992). clear truncation planes are present in S . i
included “folds” in S i have an axial surface trace that is strongly regional shear sense, determined by independent criteria, is
curved (Figs. 7.16, 7.33, 7.37). not compatible with rotation of the porphyroblasts.

2001a,b, 2002; Bell and Chen 2002) have supported the
non-rotational model. However, there are indications that
the non-rotational model is not generally valid (Passchier
et al. 1992; Visser and Mancktelow 1992; Wallis 1992; Gray
and Busa 1994; Williams 1994; Chan and Crespi 1999;
Williams and Jiang 1999; Kraus and Williams 1998, 2001;
Jiang 2001; Jiang and Williams 2004). Johnson (1993a,b)
presented a detailed study of spiral shaped inclusion
trails in garnets in order to test rotational and non-rota-
tional models and concluded that the geometries could
be explained with both models. Williams and Jiang (1999)
consider the three dimensional configuration of inclu-
sion patterns of snowball garnets a distinguishing crite-
rion and found that the application of this criterion to
all the available data favours the rotational model. How-
ever, Johnson (1999b) argues that published sections
through snowball garnets may show geometries that
Williams and Jiang (1999) consider diagnostic for non-
rotation, concluding that the rotational behaviour of
spherical porphyroblasts is still poorly understood.
Related to the study of the spatial orientation of in-
clusion patterns a special technique has been developed
to determine so called foliation intersection/inflection
axes or ‘FIA’ (Bell et al. 1998; Bell and Hickey 1997, 1999;
Hickey and Bell 1999; Bell and Mares 1999; Bell and Chen
2002). These may be rotation axes, fold hinges or inter-
section lineations between truncating planes. To deter-
mine the spatial orientation of FIA two sets of thin sec-
tions are required, one with vertical thin sections at vari-
ous strikes to determine the trend and another set fan-
ning through the horizontal to determine the plunge (see
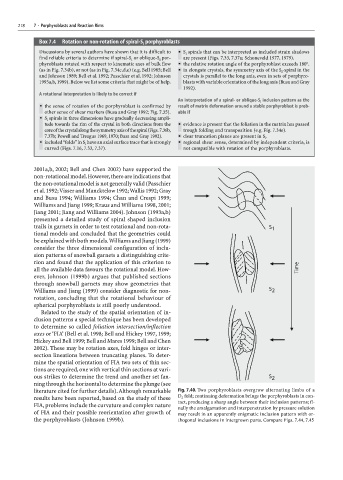
literature cited for further details). Although remarkable Fig. 7.40. Two porphyroblasts overgrow alternating limbs of a
results have been reported, based on the study of these D fold; continuing deformation brings the porphyroblasts in con-
2
tact, producing a sharp angle between their inclusion patterns; fi-
FIA, problems include the curvature and complex nature nally the amalgamation and interpenetration by pressure solution
of FIA and their possible reorientation after growth of may result in an apparently enigmatic inclusion pattern with or-
the porphyroblasts (Johnson 1999b). thogonal inclusions in intergrown parts. Compare Figs. 7.44, 7.45