Page 35 - Modelling in Transport Phenomena A Conceptual Approach

16 CHAPTER 2. MOLECULAR AND CONVECTIVE TRANSPORT

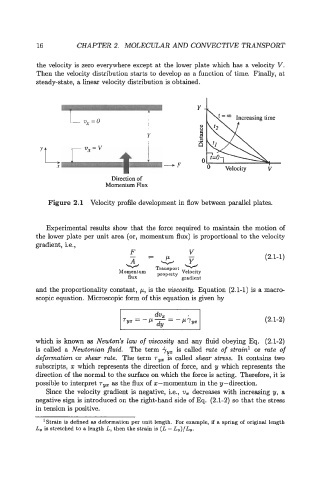
the velocity is zero everywhere except at the lower plate which has a velocity V.
Then the velocity distribution starts to develop as a function of time. Finally, at
steady-state, a linear velocity distribution is obtained.

Direction of
Momentum Flux

Figure 2.1 Velocity profile development in flow between parallel plates.

Experimental results show that the force required to maintain the motion of
- Transport - (2.1-1)
the lower plate per unit area (or, momentum flux) is proportional to the velocity
gradient, i.e.,
F
V
-
--
-
P
A
v
y
Momentum property Velocity
flux gradient
and the proportionality constant, p, is the viscosity. Equation (2.1-1) is a macro-
scopic equation. Microscopic form of this equation is given by
(2.1-2)

which is known as Newton's law of viscosity and any fluid obeying Eq. (2.1-2)
is called a Newtonian fluid. The term i., is called rate of strain' or rate of
deformation or shear rate. The term ryz is called shear stress. It contains two
subscripts, z which represents the direction of force, and y which represents the
direction of the normal to the surface on which the force is acting. Therefore, it is
possible to interpret ryx as the flux of z-momentum in the y-direction.
Since the velocity gradient is negative, i.e., v, decreases with increasing y, a
negative sign is introduced on the righbhand side of Eq. (2.1-2) so that the stress
in tension is positive.

'Strain is defined as deformation per unit length. For example, if a spring of original length
Lo is stretched to a length L, then the strain is (L - Lo)/&