Page 77 - Modern Analytical Chemistry

1400-CH04 9/8/99 3:53 PM Page 60

60 Modern Analytical Chemistry

Volumetric glassware is categorized by class. Class A glassware is manufactured
to comply with tolerances specified by agencies such as the National Institute of
Standards and Technology. Tolerance levels for class A glassware are small enough
that such glassware normally can be used without calibration. The tolerance levels
for class B glassware are usually twice those for class A glassware. Other types of vol-
umetric glassware, such as beakers and graduated cylinders, are unsuitable for accu-
rately measuring volumes.
Determinate measurement errors can be minimized by calibration. A pipet can
be calibrated, for example, by determining the mass of water that it delivers and
using the density of water to calculate the actual volume delivered by the pipet. Al-
though glassware and instrumentation can be calibrated, it is never safe to assume
that the calibration will remain unchanged during an analysis. Many instruments,
in particular, drift out of calibration over time. This complication can be minimized
by frequent recalibration.

personal error Personal Errors Finally, analytical work is always subject to a variety of personal
An error due to biases introduced by the errors, which can include the ability to see a change in the color of an indicator
analyst.
used to signal the end point of a titration; biases, such as consistently overestimat-
ing or underestimating the value on an instrument’s readout scale; failing to cali-
brate glassware and instrumentation; and misinterpreting procedural directions.
Personal errors can be minimized with proper care.

Identifying Determinate Errors Determinate errors can be difficult to detect.
Without knowing the true value for an analysis, the usual situation in any analysis
with meaning, there is no accepted value with which the experimental result can be
compared. Nevertheless, a few strategies can be used to discover the presence of a
determinate error.
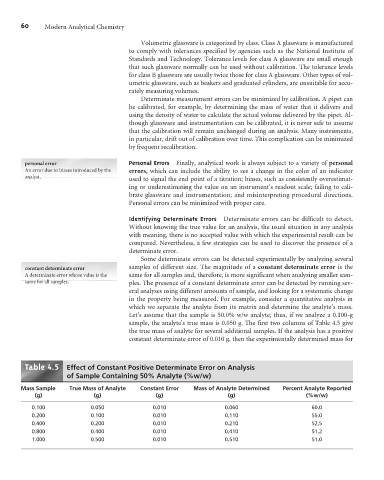
Some determinate errors can be detected experimentally by analyzing several
constant determinate error samples of different size. The magnitude of a constant determinate error is the
A determinate error whose value is the same for all samples and, therefore, is more significant when analyzing smaller sam-
same for all samples. ples. The presence of a constant determinate error can be detected by running sev-
eral analyses using different amounts of sample, and looking for a systematic change
in the property being measured. For example, consider a quantitative analysis in
which we separate the analyte from its matrix and determine the analyte’s mass.
Let’s assume that the sample is 50.0% w/w analyte; thus, if we analyze a 0.100-g
sample, the analyte’s true mass is 0.050 g. The first two columns of Table 4.5 give
the true mass of analyte for several additional samples. If the analysis has a positive
constant determinate error of 0.010 g, then the experimentally determined mass for

4 5
Table . Effect of Constant Positive Determinate Error on Analysis
of Sample Containing 50% Analyte (%w/w)
Mass Sample True Mass of Analyte Constant Error Mass of Analyte Determined Percent Analyte Reported
(g) (g) (g) (g) (%w/w)
0.100 0.050 0.010 0.060 60.0
0.200 0.100 0.010 0.110 55.0
0.400 0.200 0.010 0.210 52.5
0.800 0.400 0.010 0.410 51.2
1.000 0.500 0.010 0.510 51.0