Page 311 - Modern Control Systems

Exercises 285
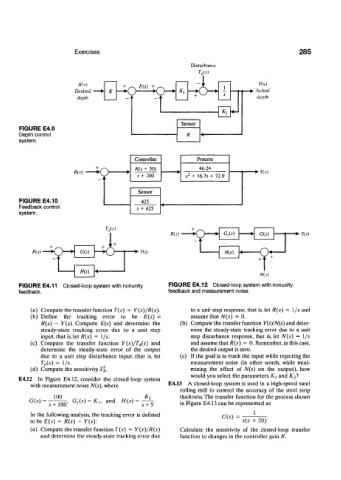
Disturbance
T/s)
R(s) Yls)
+ ^ E(s) + ^ - .
Desired t • Actual
depth depth
K,
Sensor
FIGURE E4.9
Depth control
system.

Controller Process
9" s + 200 s 2 + 16.7s + 72.9
R(s) K{s + 50) 46.24 - • Y(s)

Sensor
FIGURE E4.10 425
Feedback control
s + 425
system.

+ Y(s)

R(s) r—*>Y(s)

N(s)
FIGURE E4.11 Closed-loop system with nonunity FIGURE E4.12 Closed-loop system with nonunity
feedback. feedback and measurement noise.

(a) Compute the transfer function T(s) = Y(s)/R(s). to a unit step response, that is, let R(s) = l/s and
(b) Define the tracking error to be E(s) = assume that A/ (s) = 0.
R(s) - Y(s). Compute E(s) and determine the (b) Compute the transfer function Y(s)/N(s) and deter-
steady-state tracking error due to a unit step mine the steady-state tracking error due to a unit
input, that is, let R(s) = l/s. step disturbance response, that is, let N(s) = l/s
(c) Compute the transfer function Y(s)/T d(s) and and assume that R(s) = 0. Remember, in this case,
determine the steady-state error of the output the desired output is zero.
due to a unit step disturbance input, that is, let (c) If the goal is to track the input while rejecting the
T d(s) = l/s. measurement noise (in other words, while mini-
(d) Compute the sensitivity S' K. mizing the effect of N(s) on the output), how
would you select the parameters K\ and /C 2?
E4.12 In Figure E4.12, consider the closed-loop system
with measurement noise N(s), where E4.13 A closed-loop system is used in a high-speed steel
rolling mill to control the accuracy of the steel strip
100 Ki thickness. The transfer function for the process shown
G(s) = G c(s) = Ki. and H(s)
.v + 100' 5 + 5' in Figure E4.13 can be represented as
In the following analysis, the tracking error is defined C(s) = 1
to be £(.v) = R(s) - Y(s): s{s + 20)
(a) Compute the transfer function T(s) = Y(s)/R(.s) Calculate the sensitivity of the closed-loop transfer
and determine the steady-state tracking error due function to changes in the controller gain K.