Page 312 - Modern Control Systems

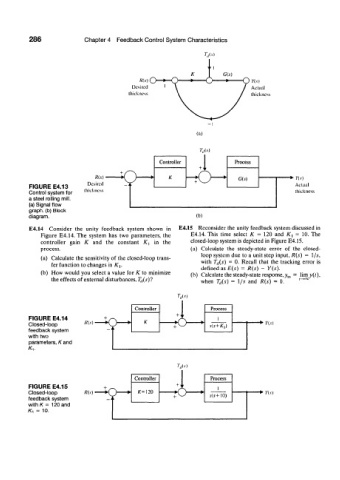
286 Chapter 4 Feedback Control System Characteristics

R(s) O Y(s)
Desired Actual
lliickness thickness

(a)

W
Controller Process
+ i r s ,
R(s) ^ , K G(5) n.v)
Desired i - < J '
FIGURE E4.13 Actual
Control system for thickness thickness
a steel rolling mill.
(a) Signal flow
graph, (b) Block
diagram. (b)
E4.14 Consider the unity feedback system shown in E4.15 Reconsider the unity feedback system discussed in
Figure E4.14. The system has two parameters, the E4.14. This time select K = 120 and K x = 10. The
controller gain K and the constant X, in the closed-loop system is depicted in Figure E4.15.
process. (a) Calculate the steady-state error of the closed-
loop system due to a unit step input, R(s) = l/s,
(a) Calculate the sensitivity of the closed-loop trans- with T d(s) = 0. Recall that the tracking error is
fer function to changes in K x.
defined as E(s) = R(s) - Y(s).
(b) How would you select a value for K to minimize (b) Calculate the steady-state response, y ss = limy(t),
the effects of external disturbances, T (i{s)7 when T a(s) = l/s and R(s) = 0. f ^°°

7 »
Controller
+
FIGURE E4.14
Closed-loop /?(.V) ' K ^ *> Y(s)
feedback system
with two
parameters, K and
Kv

7- (/(.v)

FIGURE E4.15
Closed-loop
feedback system
withK = 120 and
/C, = 10.