Page 200 - Modern Control of DC-Based Power Systems

164 Modern Control of DC-Based Power Systems

The fact that the differential equations are used directly without hav-
ing to calculate their solution gave the method its name.
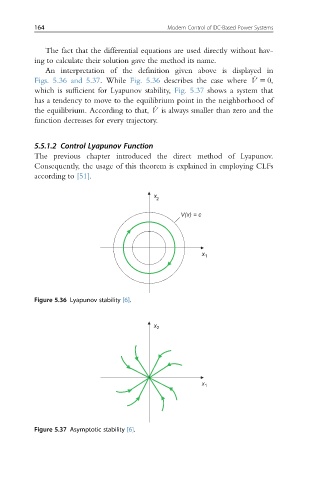
An interpretation of the definition given above is displayed in
Figs. 5.36 and 5.37. While Fig. 5.36 describes the case where _ V 5 0,
which is sufficient for Lyapunov stability, Fig. 5.37 shows a system that
has a tendency to move to the equilibrium point in the neighborhood of
_
the equilibrium. According to that, V is always smaller than zero and the
function decreases for every trajectory.

5.5.1.2 Control Lyapunov Function
The previous chapter introduced the direct method of Lyapunov.
Consequently, the usage of this theorem is explained in employing CLFs
according to [51].

x
2
V(x) = c

x 1

Figure 5.36 Lyapunov stability [6].

x 2

x 1

Figure 5.37 Asymptotic stability [6].