Page 150 - MODERN ELECTROCHEMISTRY

90 CHAPTER 2

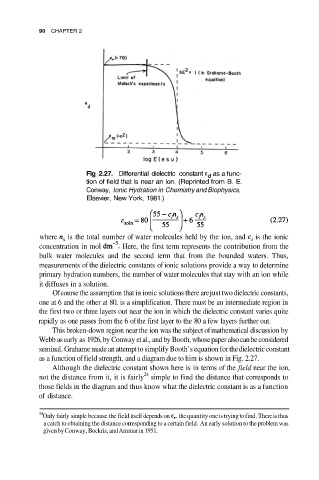
Fig 2.27. Differential dielectric constant as a func-
tion of field that is near an ion. (Reprinted from B. E.
Conway, Ionic Hydration in Chemistry and Biophysics,
Elsevier, New York, 1981.)

where is the total number of water molecules held by the ion, and is the ionic
concentration in mol Here, the first term represents the contribution from the
bulk water molecules and the second term that from the bounded waters. Thus,
measurements of the dielectric constants of ionic solutions provide a way to determine
primary hydration numbers, the number of water molecules that stay with an ion while
it diffuses in a solution.
Of course the assumption that in ionic solutions there are just two dielectric constants,
one at 6 and the other at 80, is a simplification. There must be an intermediate region in
the first two or three layers out near the ion in which the dielectric constant varies quite
rapidly as one passes from the 6 of the first layer to the 80 a few layers further out.
This broken-down region near the ion was the subject of mathematical discussion by
Webb as early as 1926, by Conway et al., and by Booth, whose paper also can be considered
seminal. Grahame made an attempt to simplify Booth’s equation for the dielectric constant
as a function of field strength, and a diagram due to him is shown in Fig. 2.27.
Although the dielectric constant shown here is in terms of the field near the ion,
24
not the distance from it, it is fairly simple to find the distance that corresponds to
those fields in the diagram and thus know what the dielectric constant is as a function
of distance.

24
Only fairly simple because the field itself depends on the quantity one is trying to find. There is thus
a catch to obtaining the distance corresponding to a certain field. An early solution to the problem was
given by Conway, Bockris, and Ammar in 1951.