Page 191 - Book Hosokawa Nanoparticle Technology Handbook

3.7 RHEOLOGY OF SLURRY FUNDAMENTALS
The critical stress at which the suspension undergoes 10 2
a transition from solids to liquids is referred to as 1.0 1.5 wt%
yield stress. The requirement for the development of
yield stress for flocculated suspensions is the forma- 1
tion of unbounded network over the system and this 10 0.7
behavior may be grounded on the same mechanism
for the appearance of plateau in dynamic viscoelastic
functions at low frequencies. 10 0
Figure 3.7.3 shows the creep and recovery behavior Viscosity η (Pa·s) 0.5
at different constant stresses for suspension with
1.0 wt% PVA in Fig. 3.7.2 [5]. 10 -1
The strain was measured as a function of time under 0.3
the condition where the stress was instantaneously
applied at t 0, maintained constant for 60 s, and sud- 10 -2
denly removed. The system responds like a viscoelastic
body at low stresses, because the time-dependent curve 0
shows instantaneous and retarded elasticity on the -3
application of stress and striking elastic recovery after 10 -2 -1 0 1 2 3
the removal of stress. When the stress is increased 10 10 10 10 10 10
·
above 2.0 Pa, the strain is increased by a factor of about Shear rate γ (s )
-1
1,000, the time-dependent profile of which is approxi-
mated by a straight line with very small recovery after Figure 3.7.4
the removal of stress. The behavior is categorized as a Effect of flocculant concentration on the viscosity
response of purely viscous liquid. Therefore, at high behavior of suspensions.
stresses the unbounded floc structures developed over
the system is considered to be broken down to a great higher viscosity than the suspensions completely
extent. Such non-linear viscoelasticity measurements dispersed to primary particles. However, the floc struc-
at various different stresses serve to evaluate the yield- tures are easily broken down in high-shear fields and
ing behavior due to the ruptures of floc structures. reversibly rebuilt in low-shear fields. As a result, the
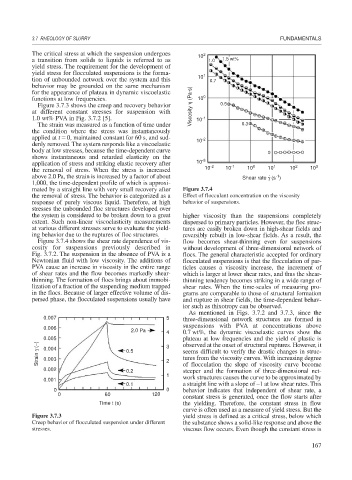
Figure 3.7.4 shows the shear rate dependence of vis- flow becomes shear-thinning even for suspensions
cosity for suspensions previously described in without development of three-dimensional network of
Fig. 3.7.2. The suspension in the absence of PVA is a flocs. The general characteristic accepted for ordinary
Newtonian fluid with low viscosity. The additions of flocculated suspensions is that the flocculation of par-
PVA cause an increase in viscosity in the entire range ticles causes a viscosity increase, the increment of
of shear rates and the flow becomes markedly shear- which is larger at lower shear rates, and thus the shear-
thinning. The formation of flocs brings about immobi- thinning tendency becomes striking in a wide range of
lization of a fraction of the suspending medium trapped shear rates. When the time-scales of measuring pro-
in the flocs. Because of larger effective volume of dis- grams are comparable to those of structural formation
persed phase, the flocculated suspensions usually have and rupture in shear fields, the time-dependent behav-
ior such as thixotropy can be observed.
As mentioned in Figs. 3.7.2 and 3.7.3, since the
0.007 5 three-dimensional network structures are formed in
suspensions with PVA at concentrations above
0.006
2.0 Pa 4 0.7 wt%, the dynamic viscoelastic curves show the
0.005 plateau at low frequencies and the yield of plastic is
Strain γ (−) 0.004 0.5 3 seems difficult to verify the drastic changes in struc-
observed at the onset of structural ruptures. However, it
tures from the viscosity curves. With increasing degree
0.003
2
0.002 0.2 of flocculation the slope of viscosity curve become
steeper and the formation of three-dimensional net-
1
0.001 work structures causes the curve to be approximated by
0.1 a straight line with a slope of –1 at low shear rates. This
0 0 behavior indicates that independent of shear rate, a
0 60 120
constant stress is generated, once the flow starts after
Time t (s) the yielding. Therefore, the constant stress in flow
curve is often used as a measure of yield stress. But the
Figure 3.7.3 yield stress is defined as a critical stress, below which
Creep behavior of flocculated suspension under different the substance shows a solid-like response and above the
stresses. viscous flow occurs. Even though the constant stress is
167