Page 362 - Book Hosokawa Nanoparticle Technology Handbook

FUNDAMENTALS CH. 6 EVALUATION METHODS FOR PROPERTIES OF NANOSTRUCTURED BODY

P max In this section, conventional analysis for indentation
loading and unloading curves to evaluate the Meyer
Loading hardness and reduced modulus of a specimen is intro-
duced. According to the recent researches on nanoin-
dentation techniques, there are several problems in the
conventional analysis to evaluate mechanical proper-
h max ties accurately. The effect of irreversible surface defor-
h c mation on indentation loading and unloading curves
should be taken into account [3,4]. Furthermore,
inverse analysis of the loading and unloading curves
[5,6] and analysis of indentation on thin films on a
substrate have progressively been studied.

A c
References
[1] W.C. Oliver, G.M. Pharr: J. Mater. Res., 7, 1564–1583
(1992).
[2] I.N. Sneddon: Int. J. Eng. Sci., 3, 47–57 (1965).
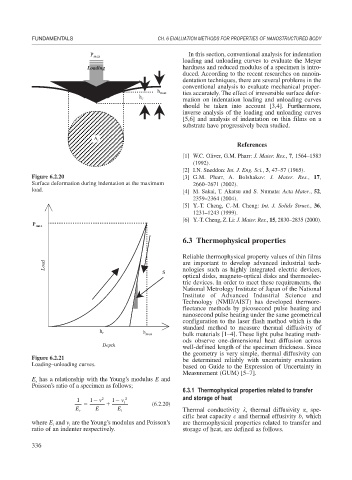
Figure 6.2.20 [3] G.M. Pharr, A. Bolshakov: J. Mater. Res., 17,
Surface deformation during indentation at the maximum 2660–2671 (2002).
load. [4] M. Sakai, T. Akatsu and S. Numata: Acta Mater., 52,
2359–2364 (2004).
[5] Y.-T. Cheng, C.-M. Cheng: Int. J. Solids Struct., 36,
1231–1243 (1999).
[6] Y.-T. Cheng, Z. Li: J. Mater. Res., 15, 2830–2835 (2000).
P max
6.3 Thermophysical properties

Reliable thermophysical property values of thin films
Load are important to develop advanced industrial tech-
S nologies such as highly integrated electric devices,
optical disks, magneto-optical disks and thermoelec-
tric devices. In order to meet these requirements, the
National Metrology Institute of Japan of the National
Institute of Advanced Industrial Science and
Technology (NMIJ/AIST) has developed thermore-
flectance methods by picosecond pulse heating and
nanosecond pulse heating under the same geometrical
configuration to the laser flash method which is the
standard method to measure thermal diffusivity of
h r h max bulk materials [1–4]. These light pulse heating meth-
ods observe one-dimensional heat diffusion across
Depth
well-defined length of the specimen thickness. Since
the geometry is very simple, thermal diffusivity can
Figure 6.2.21 be determined reliably with uncertainty evaluation
Loading–unloading curves.
based on Guide to the Expression of Uncertainty in
Measurement (GUM) [5–7].
E has a relationship with the Young’s modulus E and
r
Poisson’s ratio of a specimen as follows;
6.3.1 Thermophysical properties related to transfer
1 1 2 1 i 2 and storage of heat
(6.2.20)
E r E E i Thermal conductivity , thermal diffusivity
, spe-
cific heat capacity c and thermal effusivity b, which
where E and v are the Young’s modulus and Poisson’s are thermophysical properties related to transfer and
i
i
ratio of an indenter respectively. storage of heat, are defined as follows.
336