Page 363 - Book Hosokawa Nanoparticle Technology Handbook

6.3 THERMOPHYSICAL PROPERTIES FUNDAMENTALS
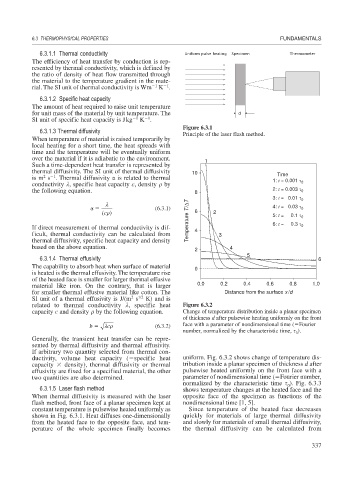
6.3.1.1 Thermal conductivity Uniform pulse heating Specimen Thermometer
The efficiency of heat transfer by conduction is rep-
resented by thermal conductivity, which is defined by
the ratio of density of heat flow transmitted through
the material to the temperature gradient in the mate-
1
rial. The SI unit of thermal conductivity is Wm 1 K .
6.3.1.2 Specific heat capacity
The amount of heat required to raise unit temperature
for unit mass of the material by unit temperature. The d
1
SI unit of specific heat capacity is Jkg 1 K .
Figure 6.3.1
6.3.1.3 Thermal diffusivity
Principle of the laser flash method.
When temperature of material is raised temporarily by
local heating for a short time, the heat spreads with
time and the temperature will be eventually uniform
over the material if it is adiabatic to the environment. 1
Such a time-dependent heat transfer is represented by
thermal diffusivity. The SI unit of thermal diffusivity 10 Time
2
1
is m s . Thermal diffusivity
is related to thermal
conductivity , specific heat capacity c, density by 1: t = 0.001 0
the following equation. 8 2: t = 0.003 0
3: t = 0.01 0

(6.3.1) 4: t = 0.03 0
(c ) 6 2 5: t = 0.1 0
If direct measurement of thermal conductivity is dif- Temperature T/ΔT 4 6: t = 0.3 0
ficult, thermal conductivity can be calculated from 3
thermal diffusivity, specific heat capacity and density
based on the above equation. 4
2
5
6.3.1.4 Thermal effusivity 6
The capability to absorb heat when surface of material 0
is heated is the thermal effusivity. The temperature rise
of the heated face is smaller for larger thermal effusive
material like iron. On the contrary, that is larger 0.0 0.2 0.4 0.6 0.8 1.0
for smaller thermal effusive material like cotton. The Distance from the surface x /d
2
SI unit of a thermal effusivity is J/(m s 1/2 K) and is
related to thermal conductivity , specific heat Figure 6.3.2
capacity c and density by the following equation. Change of temperature distribution inside a planar specimen
of thickness d after pulsewise heating uniformly on the front
b (6.3.2) face with a parameter of nondimensional time ( Fourier
c
number, normalized by the characteristic time, ).
0
Generally, the transient heat transfer can be repre-
sented by thermal diffusivity and thermal effusivity.
If arbitrary two quantity selected from thermal con-
ductivity, volume heat capacity ( specific heat uniform. Fig. 6.3.2 shows change of temperature dis-
capacity density), thermal diffusivity or thermal tribution inside a planar specimen of thickness d after
effusivity are fixed for a specified material, the other pulsewise heated uniformly on the front face with a
two quantities are also determined. parameter of nondimensional time ( Fourier number,
normalized by the characteristic time ). Fig. 6.3.3
0
6.3.1.5 Laser flash method shows temperature changes at the heated face and the
When thermal diffusivity is measured with the laser opposite face of the specimen as functions of the
flash method, front face of a planar specimen kept at nondimensional time [1, 5].
constant temperature is pulsewise heated uniformly as Since temperature of the heated face decreases
shown in Fig. 6.3.1. Heat diffuses one-dimensionally quickly for materials of large thermal diffusivity
from the heated face to the opposite face, and tem- and slowly for materials of small thermal diffusivity,
perature of the whole specimen finally becomes the thermal diffusivity can be calculated from

337