Page 104 - Numerical Analysis Using MATLAB and Excel

Exponential and Polar Forms of Phasors

2.2361

116.5651
or

x = −1; y = 2; [theta,r] = cart2pol(x,y), deg = theta*180/pi
theta =

2.0344
r =

2.2361

deg =
116.5651
Check with the Simulink model of Figure 3.11:

Figure 3.11. Simulink model for Example 3.8 (b)

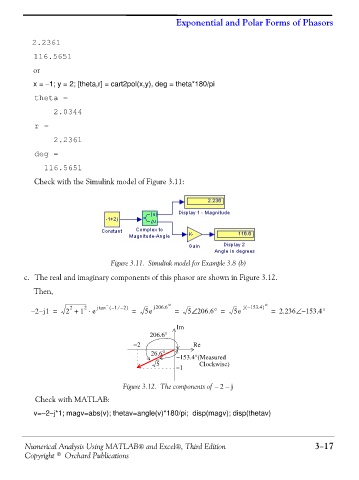
c. The real and imaginary components of this phasor are shown in Figure 3.12.
Then,

– – ( ⁄ ) j206.6° j – 153.4 °
)
(
2
2
∠
∠
– 2 j1 = 2 + 1 ⋅ e j tan 1 – 2 = 5e = 5 206.6° = 5e = 2.236 – 153.4°
–
Im
206.6°
−2 Re
26.6°
−153.4°(Measured
5 Clockwise)
−1
–
Figure 3.12. The components of 2 – j
Check with MATLAB:

v=−2−j*1; magv=abs(v); thetav=angle(v)*180/pi; disp(magv); disp(thetav)

Numerical Analysis Using MATLAB® and Excel®, Third Edition 3−17
Copyright © Orchard Publications