Page 89 - Numerical Analysis Using MATLAB and Excel

Chapter 3 Sinusoids and Phasors

As shown in Figure 3.1, the period T of an alternating current or voltage is the smallest value of
time which separates recurring values of the alternating waveform.
Unless otherwise stated, our subsequent discussion will be restricted to sine or cosine waveforms
and these are referred to as sinusoids. Two main reasons for studying sinusoids are: (1) many phys-
ical phenomena such as electric machinery produce (nearly) sinusoidal voltages and currents and
(2) by Fourier analysis, any periodic waveform which is not a sinusoid, such as the square and saw-
tooth waveforms on the previous page, can be represented by a sum of sinusoids.

3.2 Characteristics of Sinusoids

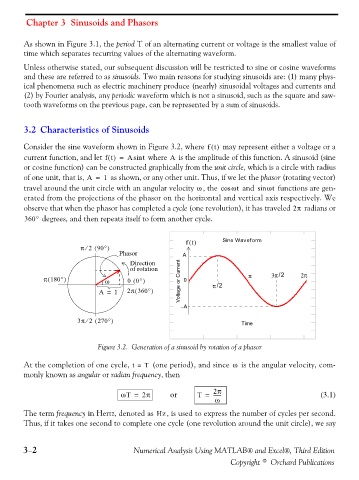
Consider the sine waveform shown in Figure 3.2, where ft() may represent either a voltage or a
A
current function, and let ft() = Asin t where is the amplitude of this function. A sinusoid (sine
or cosine function) can be constructed graphically from the unit circle, which is a circle with radius
of one unit, that is, A = 1 as shown, or any other unit. Thus, if we let the phasor (rotating vector)
ω
travel around the unit circle with an angular velocity , the cos ω t and sin ωt functions are gen-
erated from the projections of the phasor on the horizontal and vertical axis respectively. We
observe that when the phasor has completed a cycle (one revolution), it has traveled 2π radians or
360° degrees, and then repeats itself to form another cycle.

ft() Sine Waveform
(
⁄
π 2 90° )
Phasor A
Direction
of rotation
(
π 180° ) ω 0 0° ) Voltage or Current 0 π 3π /2 2π
(
(
A = 1 2π 360° ) π /2
−A

(
⁄
3π 2 270° ) Time

Figure 3.2. Generation of a sinusoid by rotation of a phasor

ω
At the completion of one cycle, t = T (one period), and since is the angular velocity, com-
monly known as angular or radian frequency, then

2π
ωT = 2π or T = ------ (3.1)
ω
The term frequency in Hertz, denoted as Hz , is used to express the number of cycles per second.
Thus, if it takes one second to complete one cycle (one revolution around the unit circle), we say

3−2 Numerical Analysis Using MATLAB® and Excel®, Third Edition
Copyright © Orchard Publications