Page 333 - Numerical Methods for Chemical Engineering

322 7 Probability theory and stochastic simulation

× 1 −
12

n w
1

= 1

n A

2

1 2
cain ent n
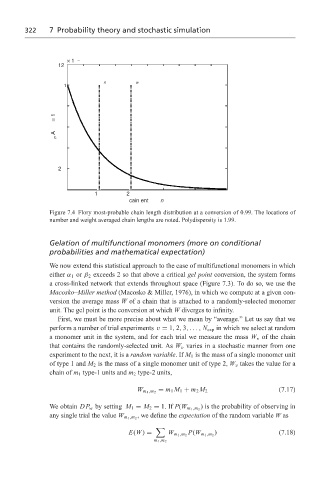
Figure 7.4 Flory most-probable chain length distribution at a conversion of 0.99. The locations of
number and weight averaged chain lengths are noted. Polydispersity is 1.99.

Gelation of multifunctional monomers (more on conditional
probabilities and mathematical expectation)

We now extend this statistical approach to the case of multifunctional monomers in which
either α 1 or β 2 exceeds 2 so that above a critical gel point conversion, the system forms
a cross-linked network that extends throughout space (Figure 7.3). To do so, we use the
Macosko–Miller method (Macosko & Miller, 1976), in which we compute at a given con-
version the average mass W of a chain that is attached to a randomly-selected monomer
unit. The gel point is the conversion at which W diverges to infinity.
First, we must be more precise about what we mean by “average.” Let us say that we
perform a number of trial experiments v = 1, 2, 3,..., N exp in which we select at random
a monomer unit in the system, and for each trial we measure the mass W v of the chain
that contains the randomly-selected unit. As W v varies in a stochastic manner from one
experiment to the next, it is a random variable.If M 1 is the mass of a single monomer unit
of type 1 and M 2 is the mass of a single monomer unit of type 2, W v takes the value for a
chain of m 1 type-1 units and m 2 type-2 units,

(7.17)
W m 1 ,m 2 = m 1 M 1 + m 2 M 2

) is the probability of observing in
We obtain DP w by setting M 1 = M 2 = 1. If P(W m 1 ,m 2
, we define the expectation of the random variable W as
any single trial the value W m 1 ,m 2

E(W) = W m 1 ,m 2 P(W m 1 ,m 2 ) (7.18)
m 1 ,m 2