Page 140 - Numerical methods for chemical engineering

126 3 Matrix eigenvalue analysis

2

1

w
−1

−2

−
λ = 12
λ =
−
1 1 2 2
cnent
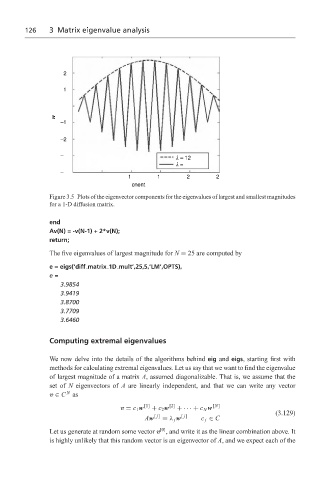
Figure 3.5 Plots of the eigenvector components for the eigenvalues of largest and smallest magnitudes
for a 1-D diffusion matrix.

end
Av(N) = -v(N-1) + 2*v(N);
return;

The five eigenvalues of largest magnitude for N = 25 are computed by
e = eigs(‘diff matrix 1D mult’,25,5,‘LM’,OPTS),
e=
3.9854
3.9419
3.8700
3.7709
3.6460

Computing extremal eigenvalues

We now delve into the details of the algorithms behind eig and eigs, starting first with
methods for calculating extremal eigenvalues. Let us say that we want to find the eigenvalue
of largest magnitude of a matrix A, assumed diagonalizable. That is, we assume that the
set of N eigenvectors of A are linearly independent, and that we can write any vector
N
v ∈ C as
v = c 1 w [1] + c 2 w [2] + ··· + c N w [N]
(3.129)
Aw [ j] = λ j w [ j] c j ∈ C
[0]
Let us generate at random some vector v , and write it as the linear combination above. It
is highly unlikely that this random vector is an eigenvector of A, and we expect each of the