Page 189 - Numerical methods for chemical engineering

Linear ODE systems and dynamic stability 175

1
er tratin r nsta e
stead state at 11
t
1 −1
−2
−
1 1 2 2
t
1
arac t secnd
1 sta e stead state
t 1
2
12

1
1 1 2 2
t
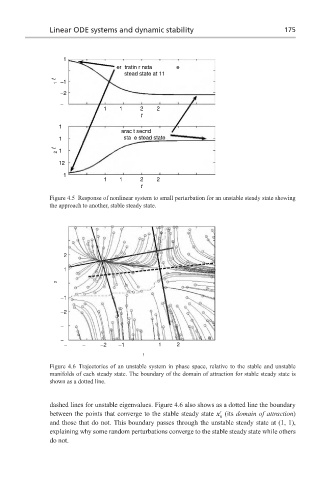
Figure 4.5 Response of nonlinear system to small perturbation for an unstable steady state showing
the approach to another, stable steady state.

2

1
2

−1
−2

−
−
− − −2 −1 1 2
1
Figure 4.6 Trajectories of an unstable system in phase space, relative to the stable and unstable
manifolds of each steady state. The boundary of the domain of attraction for stable steady state is
shown as a dotted line.

dashed lines for unstable eigenvalues. Figure 4.6 also shows as a dotted line the boundary
between the points that converge to the stable steady state x (its domain of attraction)

s
and those that do not. This boundary passes through the unstable steady state at (1, 1),
explaining why some random perturbations converge to the stable steady state while others
do not.