Page 305 - Origin and Prediction of Abnormal Formation Pressures

PORE WATER COMPACTION CHEMISTRY AS RELATED TO OVERPRESSURES 275

10,000 -

E \ ~ ,CI
C).
CL
c- "'"'~'--x \" Na +
O k
1000 -
,m,,,
\ ~ t~,,,,2 +
0
C}. ~%~' -'---e h A _2+
E ~. S. _e ,/+
0 \.. ..,(,"
0 "~-.-,...,, ./ \
0 ~'~..~/ ~
0 100 " %
E \ SO4 2
(b
r
(,9

seo ~oter i 1'2 2~,

Compaction time, days
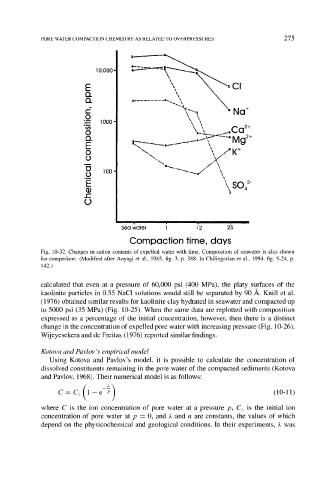
Fig. 10-32. Changes in cation contents of expelled water with time. Composition of seawater is also shown
for comparison. (Modified after Aoyagi et al., 1985, fig. 3, p. 388. In Chilingarian et al., 1994, fig. 5-24, p.
142.)

calculated that even at a pressure of 60,000 psi (400 MPa), the platy surfaces of the
kaolinite particles in 0.55 NaC1 solutions would still be separated by 90/k. Knill et al.
(1976) obtained similar results for kaolinite clay hydrated in seawater and compacted up
to 5000 psi (35 MPa) (Fig. 10-25). When the same data are replotted with composition
expressed as a percentage of the initial concentration, however, then there is a distinct
change in the concentration of expelled pore water with increasing pressure (Fig. 10-26).
Wijeyesekera and de Freitas (1976) reported similar findings.

Kotova and Pavlov's empirical model
Using Kotova and Pavlov's model, it is possible to calculate the concentration of
dissolved constituents remaining in the pore water of the compacted sediments (Kotova
and Pavlov, 1968). Their numerical model is as follows:

C--Co 1 e p (10-11)

where C is the ion concentration of pore water at a pressure p, Co is the initial ion
concentration of pore water at p = O, and )~ and n are constants, the values of which
depend on the physicochemical and geological conditions. In their experiments, )~ was