Page 289 - PRINCIPLES OF QUANTUM MECHANICS as Applied to Chemistry and Chemical Physics

280 Molecular structure

U (R)

R e
0
R

2D e
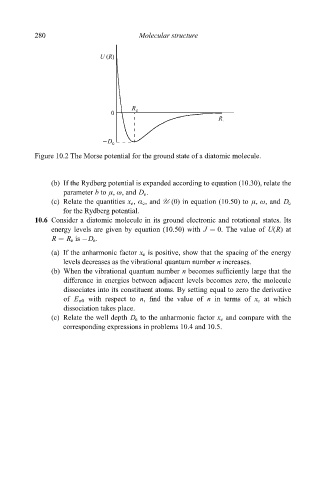
Figure 10.2 The Morse potential for the ground state of a diatomic molecule.

(b) If the Rydberg potential is expanded according to equation (10.30), relate the
parameter b to ì, ù, and D e .
(c) Relate the quantities x e , á e , and U (0) in equation (10.50) to ì, ù, and D e
for the Rydberg potential.
10.6 Consider a diatomic molecule in its ground electronic and rotational states. Its
energy levels are given by equation (10.50) with J ˆ 0. The value of U(R)at
R ˆ R e is ÿD e .

(a) If the anharmonic factor x e is positive, show that the spacing of the energy
levels decreases as the vibrational quantum number n increases.
(b) When the vibrational quantum number n becomes suf®ciently large that the
difference in energies between adjacent levels becomes zero, the molecule
dissociates into its constituent atoms. By setting equal to zero the derivative
of E n0 with respect to n, ®nd the value of n in terms of x e at which
dissociation takes place.
(c) Relate the well depth D e to the anharmonic factor x e and compare with the
corresponding expressions in problems 10.4 and 10.5.