Page 162 - Phase Space Optics Fundamentals and Applications

The Radon-Wigner Transform 143

1.0 p = 0.5 1.0 p = 0.5
W 20 /λ = 0.99 W 20 /λ = 0.99

0.0 0.0
ξ ξ
0.00 0.00

1.0 p = 0.75 1.0 p = 0.75
W 20 /λ = 0.40 W 20 /λ = 0.40
OTF OTF

0.0 0.0
ξ ξ
0.00 0.00

1.0 p = 1 1.0 p = 1
W 20 /λ = 0 W 20 /λ = 0

0.0 0.0
ξ ξ
0.00 0.00

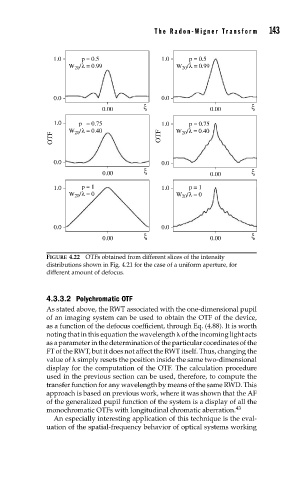
FIGURE 4.22 OTFs obtained from different slices of the intensity
distributions shown in Fig. 4.21 for the case of a uniform aperture, for
different amount of defocus.

4.3.3.2 Polychromatic OTF
As stated above, the RWT associated with the one-dimensional pupil
of an imaging system can be used to obtain the OTF of the device,
as a function of the defocus coefficient, through Eq. (4.88). It is worth
noting that in this equation the wavelength of the incoming light acts
as a parameter in the determination of the particular coordinates of the
FT of the RWT, but it does not affect the RWT itself. Thus, changing the
value of simply resets the position inside the same two-dimensional
display for the computation of the OTF. The calculation procedure
used in the previous section can be used, therefore, to compute the
transfer function for any wavelength by means of the same RWD. This
approach is based on previous work, where it was shown that the AF
of the generalized pupil function of the system is a display of all the
monochromatic OTFs with longitudinal chromatic aberration. 43
An especially interesting application of this technique is the eval-
uation of the spatial-frequency behavior of optical systems working