Page 161 - Phase Space Optics Fundamentals and Applications

142 Chapter Four

Thus, by using Eq. (4.22) it is easy to find that
F {RW t (x , ), } = A t ( cos , − sin )
2
cos h
= H − ; W 20 = tan (4.88)
( f + z) 2
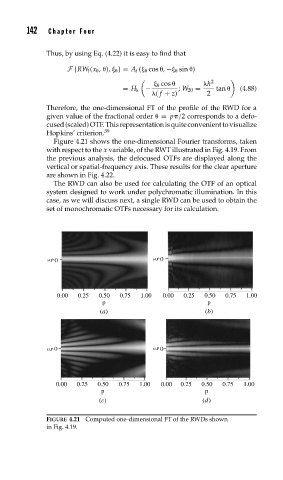
Therefore, the one-dimensional FT of the profile of the RWD for a
given value of the fractional order = p /2 corresponds to a defo-
cused(scaled)OTF.Thisrepresentationisquiteconvenienttovisualize
Hopkins’ criterion. 39
Figure 4.21 shows the one-dimensional Fourier transforms, taken
with respect to the x variable, of the RWT illustrated in Fig. 4.19. From
the previous analysis, the defocused OTFs are displayed along the
vertical or spatial-frequency axis. These results for the clear aperture
are shown in Fig. 4.22.
The RWD can also be used for calculating the OTF of an optical
system designed to work under polychromatic illumination. In this
case, as we will discuss next, a single RWD can be used to obtain the
set of monochromatic OTFs necessary for its calculation.

0 ξ 0 ξ

0.00 0.25 0.50 0.75 1.00 0.00 0.25 0.50 0.75 1.00
p p
(a) (b)

0 ξ ξ 0

0.00 0.25 0.50 0.75 1.00 0.00 0.25 0.50 0.75 1.00
p p
(c) (d)

FIGURE 4.21 Computed one-dimensional FT of the RWDs shown
in Fig. 4.19.