Page 162 - Physical Principles of Sedimentary Basin Analysis

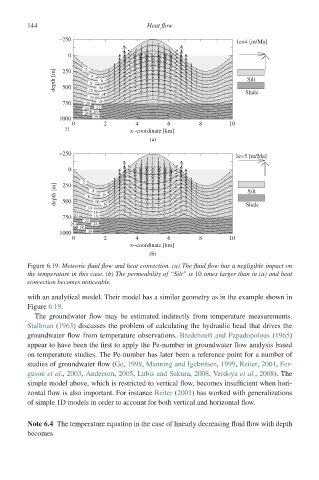
144 Heat flow

−250 1e+4 [m/Ma]
0
2
4 2
depth [m] 8 4 6 Silt
250
500
10
12
14 Shale
16
750 20 18 22
24 22
28 26 36 34
1000 30 38
0 2 4 6 8 10
22 x−coordinate [km]
(a)
−250
1e+5 [m/Ma]
0
2 4
2
depth [m] 250 8 4 6 6 Silt
500
14 10 12 Shale
16
20 20 18 22
750
22
26 24 24
28
1000 30 34
0 2 4 6 8 10
x−coordinate [km]
(b)
Figure 6.19. Meteoric fluid flow and heat convection. (a) The fluid flow has a negligible impact on
the temperature in this case. (b) The permeability of “Silt” is 10 times larger than in (a) and heat
convection becomes noticeable.
with an analytical model. Their model has a similar geometry as in the example shown in
Figure 6.19.
The groundwater flow may be estimated indirectly from temperature measurements.
Stallman (1963) discusses the problem of calculating the hydraulic head that drives the
groundwater flow from temperature observations. Bredehoeft and Papadopolous (1965)
appear to have been the first to apply the Pe-number in groundwater flow analysis based
on temperature studies. The Pe-number has later been a reference point for a number of
studies of groundwater flow (Ge, 1998, Manning and Igebritsen, 1999, Reiter, 2001, Fer-
guson et al., 2003, Anderson, 2005, Lubis and Sakura, 2008, Verdoya et al., 2008). The
simple model above, which is restricted to vertical flow, becomes insufficient when hori-
zontal flow is also important. For instance Reiter (2001) has worked with generalizations
of simple 1D models in order to account for both vertical and horizontal flow.

Note 6.4 The temperature equation in the case of linearly decreasing fluid flow with depth
becomes