Page 166 - Physical Principles of Sedimentary Basin Analysis

148 Heat flow

1.0

0.8 ^ t=0.08 ^ t=infinity

0.6 ^ t=0.02
^ t=0.04
z [−] t=0
^
^
0.4
0.2

0.0
0.0 0.2 0.4 0.6 0.8 1.0
^
T [−]
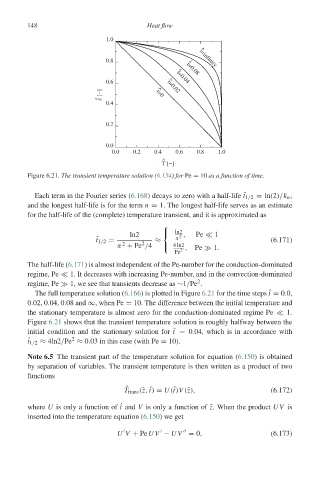
Figure 6.21. The transient temperature solution (6.154)for Pe = 10 as a function of time.

Each term in the Fourier series (6.168) decays to zero with a half-life ˆ t 1/2 = ln(2)/k n ,
and the longest half-life is for the term n = 1. The longest half-life serves as an estimate
for the half-life of the (complete) temperature transient, and it is approximated as

⎧
ln2
ln2 ⎨ 2 , Pe
1
ˆ t 1/2 = ≈ π (6.171)
2
2
π + Pe /4 ⎩ 4 ln2 , Pe
1.
Pe 2
The half-life (6.171) is almost independent of the Pe-number for the conduction-dominated
regime, Pe
1. It decreases with increasing Pe-number, and in the convection-dominated
2
regime, Pe
1, we see that transients decrease as ∼1/Pe .
The full temperature solution (6.166) is plotted in Figure 6.21 for the time steps ˆ t = 0.0,
0.02, 0.04, 0.08 and ∞, when Pe = 10. The difference between the initial temperature and
the stationary temperature is almost zero for the conduction-dominated regime Pe
1.
Figure 6.21 shows that the transient temperature solution is roughly halfway between the
initial condition and the stationary solution for ˆ t = 0.04, which is in accordance with
2
ˆ t 1/2 ≈ 4ln2/Pe ≈ 0.03 in this case (with Pe = 10).
Note 6.5 The transient part of the temperature solution for equation (6.150) is obtained
by separation of variables. The transient temperature is then written as a product of two
functions

ˆ
T trans (ˆz, ˆ t) = U(ˆ t)V (ˆz), (6.172)
where U is only a function of ˆ t and V is only a function of ˆz. When the product UV is
inserted into the temperature equation (6.150) we get

U V + Pe UV − UV = 0, (6.173)