Page 274 - Physical Chemistry

lev38627_ch08.qxd 3/14/08 12:54 PM Page 255

255
( P/ T) a/k [Eq. (1.45)]. Experiment shows ( P/ T) is finite and positive at the Section 8.7
V m V m
2
critical point. Therefore, a q at the critical point. We have C P,m C V,m TV a /k The Law of Corresponding States
m
C V,m TV a( P/ T) V m [Eq. (4.53)]. Since a q at the critical point, it follows that
m
C P,m q at the critical point. Figure 8.7 plots c for saturated liquid water and for satu-
P
rated water vapor versus T. (Recall Fig. 7.2, which plots r of each of the saturated
phases.) As the critical point (374°C, 218 atm) is approached, C P,m of each phase goes to
infinity. For points close to the critical point, C P,m is quite large. This explains the large
maxima in c of H O(g)on the 400°C isotherm and the 300-bar isobar in Fig. 2.5.
2
P
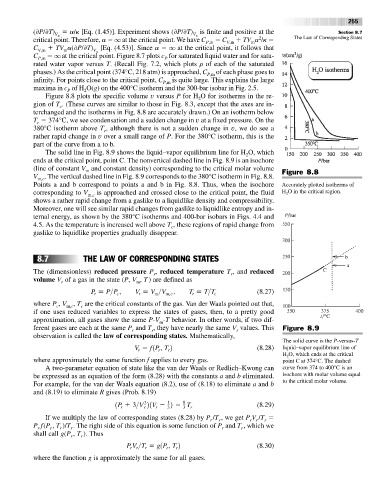
Figure 8.8 plots the specific volume v versus P for H O for isotherms in the re-
2
gion of T . (These curves are similar to those in Fig. 8.3, except that the axes are in-
c
terchanged and the isotherms in Fig. 8.8 are accurately drawn.) On an isotherm below
T 374°C, we see condensation and a sudden change in v at a fixed pressure. On the
c
380°C isotherm above T , although there is not a sudden change in v, we do see a
c
rather rapid change in v over a small range of P. For the 380°C isotherm, this is the
part of the curve from a to b.
The solid line in Fig. 8.9 shows the liquid–vapor equilibrium line for H O, which
2
ends at the critical point, point C. The nonvertical dashed line in Fig. 8.9 is an isochore
(line of constant V and constant density) corresponding to the critical molar volume Figure 8.8
m
V . The vertical dashed line in Fig. 8.9 corresponds to the 380°C isotherm in Fig. 8.8.
m,c
Points a and b correspond to points a and b in Fig. 8.8. Thus, when the isochore Accurately plotted isotherms of
corresponding to V m,c is approached and crossed close to the critical point, the fluid H O in the critical region.
2
shows a rather rapid change from a gaslike to a liquidlike density and compressibility.
Moreover, one will see similar rapid changes from gaslike to liquidlike entropy and in-
ternal energy, as shown by the 380°C isotherms and 400-bar isobars in Figs. 4.4 and
4.5. As the temperature is increased well above T , these regions of rapid change from
c
gaslike to liquidlike properties gradually disappear.
8.7 THE LAW OF CORRESPONDING STATES

The (dimensionless) reduced pressure P , reduced temperature T , and reduced
r
r
volume V of a gas in the state (P, V , T) are defined as
r
m
P P>P , V V >V m,c , T T>T c (8.27)
r
m
r
c
r
where P , V , T are the critical constants of the gas. Van der Waals pointed out that,
c
m,c
c
if one uses reduced variables to express the states of gases, then, to a pretty good
approximation, all gases show the same P-V -T behavior. In other words, if two dif-
m
ferent gases are each at the same P and T , they have nearly the same V values. This Figure 8.9
r
r
r
observation is called the law of corresponding states. Mathematically,
The solid curve is the P-versus-T
V f1P , T 2 (8.28) liquid–vapor equilibrium line of
r
r
r
H O, which ends at the critical
2
where approximately the same function f applies to every gas. point C at 374°C. The dashed
A two-parameter equation of state like the van der Waals or Redlich–Kwong can curve from 374 to 400°C is an
be expressed as an equation of the form (8.28) with the constants a and b eliminated. isochore with molar volume equal
For example, for the van der Waals equation (8.2), use of (8.18) to eliminate a and b to the critical molar volume.
and (8.19) to eliminate R gives (Prob. 8.19)
8
1
2
1P 3>V 21V 2 T r (8.29)
3
3
r
r
r
If we multiply the law of corresponding states (8.28) by P /T , we get P V /T
r
r r
r
r
P f(P , T )/T . The right side of this equation is some function of P and T , which we
r
r
r
r
r
r
shall call g(P , T ). Thus
r
r
P V >T g1P , T 2 (8.30)
r
r
r
r r
where the function g is approximately the same for all gases.