Page 375 - Physical Chemistry

lev38627_ch12.qxd 3/18/08 2:41 PM Page 356

356
Chapter 12 where the total solute molality is m
i A m . Note that T is independent of the
tot
i
f
Multicomponent Phase Equilibrium
nature of the species in solution and depends only on the total molality, provided the
solution is dilute enough to be considered ideally dilute.
For electrolyte solutions, one cannot use (12.17), since an electrolyte solution
only becomes ideally dilute at molalities too low to produce a measurable T . One
f
must retain g in (12.7) for electrolyte solutions. (See Prob. 12.13.) In the crudest ap-
A
proximation with g 1, we would expect from (12.17) that an electrolyte like NaCl
A
that yields two ions in solution would give roughly twice the freezing-point depres-
sion as a nonelectrolyte at the same molality.
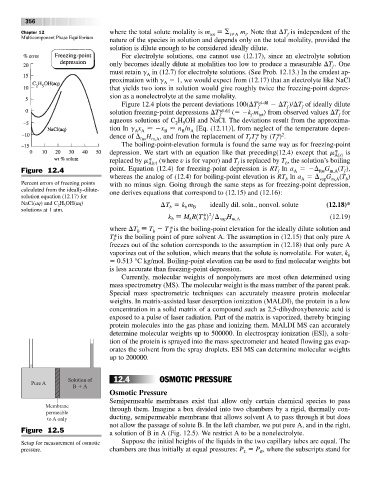
Figure 12.4 plots the percent deviations 100( T id-dil T )/ T of ideally dilute
f f f
solution freezing-point depressions T id-dil ( k m ) from observed values T for
f f tot f
aqueous solutions of C H OH and NaCl. The deviations result from the approxima-
2 5
tion ln g x x n /n [Eq. (12.11)], from neglect of the temperature depen-
A A B B A
2
dence of H , and from the replacement of T T* by (T*) .
fus m,A f f f
The boiling-point-elevation formula is found the same way as for freezing-point
depression. We start with an equation like that preceding(12.4) except that m* is
A(s)
replaced by m* (where v is for vapor) and T is replaced by T , the solution’s boiling
A(v) f b
Figure 12.4 point. Equation (12.4) for freezing-point depression is RT ln a G m,A (T ),
f
f
A
fus
whereas the analog of (12.4) for boiling-point elevation is RT ln a G m,A (T )
b
A
vap
b
Percent errors of freezing points with no minus sign. Going through the same steps as for freezing-point depression,
calculated from the ideally-dilute- one derives equations that correspond to (12.15) and (12.16):
solution equation (12.17) for
NaCl(aq) and C H OH(aq) ¢T k m ideally dil. soln., nonvol. solute (12.18)*
5
2
b
B
b
solutions at 1 atm.
2
k M R1T*2 >¢ vap H m,A (12.19)
A
b
b
where T T T*is the boiling-point elevation for the ideally dilute solution and
b b b
T*is the boiling point of pure solvent A. The assumption in (12.15) that only pure A
b
freezes out of the solution corresponds to the assumption in (12.18) that only pure A
vaporizes out of the solution, which means that the solute is nonvolatile. For water, k
b
0.513 °C kg/mol. Boiling-point elevation can be used to find molecular weights but
is less accurate than freezing-point depression.
Currently, molecular weights of nonpolymers are most often determined using
mass spectrometry (MS). The molecular weight is the mass number of the parent peak.
Special mass spectrometric techniques can accurately measure protein molecular
weights. In matrix-assisted laser desorption ionization (MALDI), the protein in a low
concentration in a solid matrix of a compound such as 2,5-dihydroxybenzoic acid is
exposed to a pulse of laser radiation. Part of the matrix is vaporized, thereby bringing
protein molecules into the gas phase and ionizing them. MALDI MS can accurately
determine molecular weights up to 500000. In electrospray ionization (ESI), a solu-
tion of the protein is sprayed into the mass spectrometer and heated flowing gas evap-
orates the solvent from the spray droplets. ESI MS can determine molecular weights
up to 200000.
Solution of 12.4 OSMOTIC PRESSURE
Pure A
B A
Osmotic Pressure
Semipermeable membranes exist that allow only certain chemical species to pass
Membrane through them. Imagine a box divided into two chambers by a rigid, thermally con-
permeable
to A only ducting, semipermeable membrane that allows solvent A to pass through it but does
not allow the passage of solute B. In the left chamber, we put pure A, and in the right,
Figure 12.5
a solution of B in A (Fig. 12.5). We restrict A to be a nonelectrolyte.
Setup for measurement of osmotic Suppose the initial heights of the liquids in the two capillary tubes are equal. The
pressure. chambers are thus initially at equal pressures: P P , where the subscripts stand for
L R