Page 389 - Physical Chemistry

lev38627_ch12.qxd 3/18/08 2:41 PM Page 370

370
Chapter 12 of this chapter. All points between J and K on the tie line correspond to states with the
b
a
Multicomponent Phase Equilibrium same value of x and the same x .
B
B
12.7 TWO-COMPONENT LIQUID–LIQUID EQUILIBRIUM
When any amounts of ethanol and water are shaken together in a separatory funnel at
room temperature, one always obtains a single-phase liquid system. Ethanol and water
are soluble in each other to unlimited extents and are said to be completely miscible.
When roughly equal amounts of 1-butanol and water are shaken together at room tem-
perature, one obtains a system consisting of two liquid phases: one phase is water con-
taining a small amount of dissolved 1-butanol, and the other is 1-butanol containing a
small amount of dissolved water. These two liquids are partially miscible, meaning
that each is soluble in the other to a limited extent.
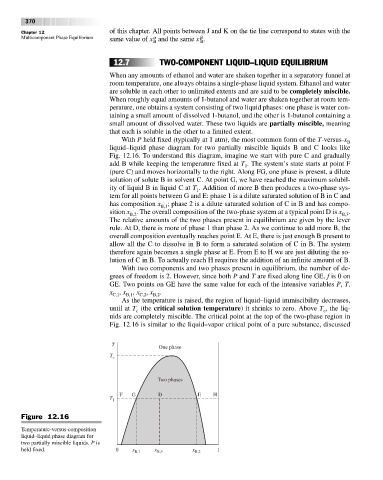
With P held fixed (typically at 1 atm), the most common form of the T-versus-x B
liquid–liquid phase diagram for two partially miscible liquids B and C looks like
Fig. 12.16. To understand this diagram, imagine we start with pure C and gradually
add B while keeping the temperature fixed at T . The system’s state starts at point F
1
(pure C) and moves horizontally to the right. Along FG, one phase is present, a dilute
solution of solute B in solvent C. At point G, we have reached the maximum solubil-
ity of liquid B in liquid C at T . Addition of more B then produces a two-phase sys-
1
tem for all points between G and E: phase 1 is a dilute saturated solution of B in C and
has composition x ; phase 2 is a dilute saturated solution of C in B and has compo-
B,1
sition x . The overall composition of the two-phase system at a typical point D is x .
B,3
B,2
The relative amounts of the two phases present in equilibrium are given by the lever
rule. At D, there is more of phase 1 than phase 2. As we continue to add more B, the
overall composition eventually reaches point E. At E, there is just enough B present to
allow all the C to dissolve in B to form a saturated solution of C in B. The system
therefore again becomes a single phase at E. From E to H we are just diluting the so-
lution of C in B. To actually reach H requires the addition of an infinite amount of B.
With two components and two phases present in equilibrium, the number of de-
grees of freedom is 2. However, since both P and T are fixed along line GE, f is 0 on
GE. Two points on GE have the same value for each of the intensive variables P, T,
x , x , x , x .
B,1
C,2
C,1
B,2
As the temperature is raised, the region of liquid–liquid immiscibility decreases,
until at T (the critical solution temperature)it shrinks to zero. Above T , the liq-
c
c
uids are completely miscible. The critical point at the top of the two-phase region in
Fig. 12.16 is similar to the liquid–vapor critical point of a pure substance, discussed
T
One phase
T c

Two phases

F G D E H
T 1

Figure 12.16
Temperature-versus-composition
liquid–liquid phase diagram for
two partially miscible liquids. P is
held fixed. 0 x B,1 x B,3 x B,2 1