Page 212 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

186 Chapter Seven

0.9 r;:::::::;:~::::::::~:::::::::==:::::;--:--.--~-:-~
-Outlet temperature
0.8 Undelayed component .. · ... ;.:.-··:·
. -.Delayed component
0.7 •• ·.t
~ 0.6
-; Uc = 1 L = 1 v = 1
R. 0.5
e rr = 1
~ 0.4
~ t 0 /rr = 1
:s 0.3
0
0.2

0
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Tune
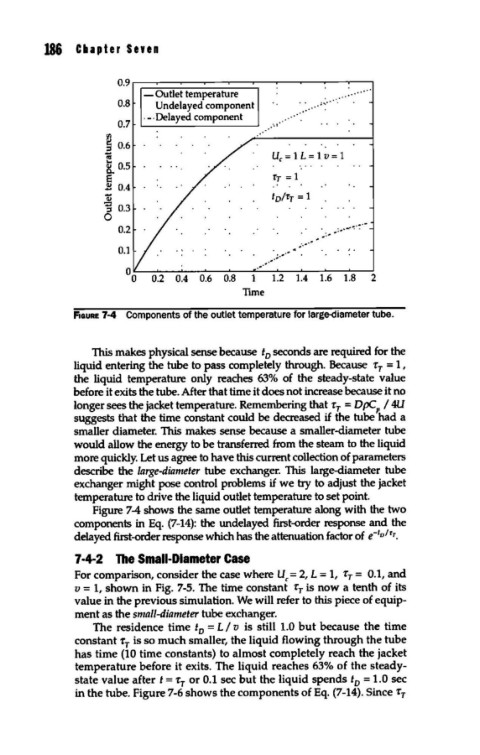
FIGURE 7-4 Components of the outlet temperature for large-diameter tube.

This makes physical sense because t seconds are required for the
0
liquid entering the tube to pass completely through. Because rr = 1 ,
the liquid temperature only reaches 63% of the steady-state value
before it exits the tube. After that time it does not increase because it no
longer sees the jacket temperature. Remembering that rr = DpCP. I 4U
suggests that the time constant could be decreased if the tube had a
smaller diameter. This makes sense because a smaller-diameter tube
would allow the energy to be transferred from the steam to the liquid
more quickly. Let us agree to have this current collection of parameters
describe the large-diameter tube exchanger. This large-diameter tube
exchanger might pose control problems if we try to adjust the jacket
temperature to drive the liquid outlet temperature to set point.
Figure 7-4 shows the same outlet temperature along with the two
components in Eq. (7-14): the undelayed first-order response and the
delayed first-order response which has the attenuation factor of e-to/rr.

7-4-2 The Small-Diameter Case
For comparison, consider the case where Uc= 2, L = 1, rr = 0.1, and
v = 1, shown in Fig. 7-5. The time constant rr is now a tenth of its
value in the previous simulation. We will refer to this piece of equip-
ment as the small-diameter tube exchanger.
The residence time t = L I v is still 1.0 but because the time
0
constant rr is so much smaller, the liquid flowing through the tube
has time (10 time constants) to almost completely reach the jacket
temperature before it exits. The liquid reaches 63% of the steady-
state value after t = rr or 0.1 sec but the liquid spends t = 1.0 sec
0
in the tube. Figure 7-6 shows the components of Eq. (7-14). Since rr