Page 52 - Pressure Swing Adsorption

26 PRESSURE SWING ADSORPTION FUNDAMENTALS OF ADSORPTION 27

Favorable
0.8 7
~ 193 K
0.6
6
qo- "o 0.4 0
5
Unfavorable
"" 0
0.2 0.4 0.6 0.8 1.0 :; N2 02
4 Adsorption D 0
en /
C Desorption Ill •
"D
ro 3
Figure 2.10 Dimcnsmnlcss cquilibnum isotherm shi:.1wrng the mcanmg of the terms _,
0
"favorahle." "linear," and "unfavorable."
2
This form may be denved from s1mole mass action considerations t)y consid- 273 K
ering the balance between occupied and unoccupied sites. Equation 2.3
clearly shows the correct asymptotic behavior since 1t approaches Hemys
Law in the low-concentrat1on region ancl the saturation limit {q ......_. qJ at high
concentrations. In the onginal Langmuir formulation the saiurat1011 limit was 0 300 400 500 600 700 800
assumed to coincide with saturation of a fixed number of identical surface
P(torr)
sites and. as such. It should he mdcncndcnt of tcmneraturc. In faci a modest
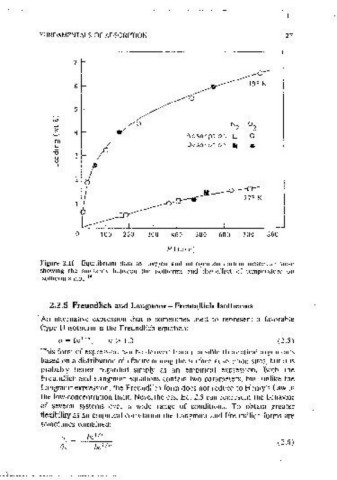
decrease of q~ with temperature 1s generally observed and 1s indeed to be Figure 2.11 Euuilibnum data for oxygen and nitrogen .on carbon molecular sieve
expected if the saturation limit corresponds with filling of the m,cropore showmg tile s1milantv between the 1sot11erms and the: effect of temperature on
14
voiume, rather than with the saturation of a set of surface sites. b 1s an isotherm shape.
equilibnum constant that 1s directly related to the Henry constant (K = bq).
Since adsorption is exothermic, 1t follows that b, like K, will decrease with
temperature so at higher temperature the isotherms become less sharply 2.2.5 Freundlich and Langmuir - Freundlich Isotherms
curved, as illustrated in Figure 2.11.
An alternative expression that is sometimes used to represent a favorable
The 1soster1c enthalpy of sorpt1on is given by:
(type I) isotherm 1s the Freundlich eauat1on:
a - bc:'I", n > 1.0 (2.5)
( 2.4)
This form of expression can be derived from plau!->iblc theoretical arguments
based on a distrihut10n of aflinity among the surface' adsomt1on sites, bur 1t 1s
and it follows from Eqs. 2.3 and 2.4 that if q 1s independent of temperature,
5 probably better regarded simply as an empmcal expression. Both the
the 1sostenc heat will be independent of concentrat1on~a well-known fea-
Freundlich and Langmulf equations contain two parameters, but, unlike the
ture of idcai Langmulf behavior.
Langmutr expression, the Freundlich form does not reduce to Henry·s Law m
Although there are relauveiy few systems that conform accurately io the
the low-concentration limit. Nevertheless, Ea. 2.5 can reoresent the behavior
Langmuir model, there are a great many systems that show approximate
of several systems over a wide range of condit10ns. To obtain greater
conformity, and this model has the further advantage that It reduces to
flexibility as an empmcal correlat1on the Langmuir and Freundlich forms are
Henry's Law m the low~concentration limit, which ts a requirement for
sometimes combined:
thermodynamic consistency in any physical adsorpt10n system. For these
reasons the Langmuir modci has hccl)nlc widely accented as the basis for a hc1111
most quc.1litat1vc or sem1qu;inr1tat1ve studies of PSA systems. qs I + bc 11 " (2.6)