Page 81 - Pressure Swing Adsorption

56 PRESSURE SWING ADSORPTION FUNDAMENTALS OF ADSORPTION 57

shock form. On the other hand, if mass transfer resistance and/or axiai
m1xmg effects are large, the distance reqmred to :approach the constant
oattern limit will be large and the form of the asymritotlc oroflle will be
correspondingly dispersed.
As with the unfavorable case, both the form of the asymptotic profile and
the distance required to approac11 this limit are also affected by the curvature
of the isotherm. When the isotherm 1s strongiy curved (highly favorable), the
asymptotic limit will be approached rapidly and will be correspondingly
sharp, whereas where the isotherm 1s of only slightiv favorable form. the
asymptotic profile will be reached only m a very long column and will be
correspondingly disoersed. It 1s evident that, m the case of an isotherm with
an mflection, where equilibnum theory predicts a composite wave one mav
expect to see m practice a combinatmn of constant pattern and proportionate
pattern profiles as the asymptotic waveform.

2.4.3 Linear Systems
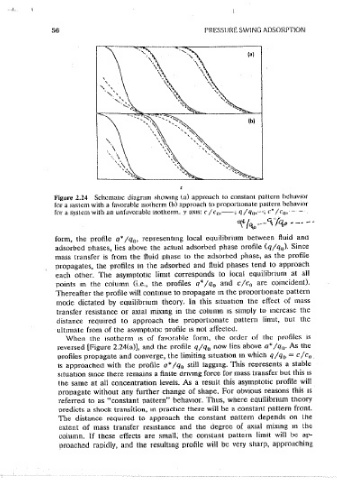
Figure 2.24 Schematic diagram showing (a) approach to constam pattern hcbavmr When the JSotherm is iinear, cquilibnum thcorv predicts that the profile will
for a svstcm with a favorable isotherm (h) approach to proportmnate pattern behavior
oropagate withoui change of shape. The effect of mass transfer resistance
for a system with an unfavorable isotherm. _v axis: c/c 0 ,--; q/q 0 ,~--; c"' /c 0 ,-- -
'\"lei.,---'\ ·ra.o --· -· and ax1ai dispersion is to cause the profile tn spread as 1t orooagates.
Detailed analysis (see the following) shows that the spread of the profile
form, the profile a* /q , reoresentmg local equilibrium between fluid anct mcreases m oroport10n to the square root of distance {or time). There is no
0
adsorbed phases, lies above the actual adsorbed phase profile (q/q 11 ). Since asymptotic limit; such behavmr contmues rndefinitelv.
mass transfer is from the fluid phase to the adsorbed phase, as the profile
propagates, the profiles in the adsorbed and fluid phases tend to approach 2.4.4 Dynamic Modeling
each other. The asymptotic limit corresponds to iocal equilibrium at all
points m the coiumn (i.e., the profiles a°"' /q and c/c 0 are coincident). Knowledge of the asymptotic profile forms 1s helpful m understanding the
0
Thereafter the profile will contmue to propagate m the proportionate pattern dynamic behavior of an adsorotmn column, but m most PSA systems the
mode dictated by equilibnum theory. In this s1tuat10n the effect of mass column length and cycle time are not sufficiently long or the isotherm
sufficiently strongly curved for the asymotottc profiles to be closetv ap-
transfer resistance or axial mixmg m the column 1s simply to mcrease the
distance required to approach the proportionate pattern limit, but the proached. To model the dynamic behavior a 1s therefore necessary to solve
ultimate from of the asvmptot1c profile 1s not affected. s1multaneously the differential fluid phase mass balance for the column with
the appropriate adsorption rate expression. If heat effects arc significant, the
When tile isotherm 1s of favorable form, the order of the profiles is
problem becomes even more difficuit, smce 1t is thc:n necessary also to solve
reversed (Figure 2.24(a)], and the profile q/q now lies above a* /q 0 • As the
0
the differential heat balance equation. lhe general formulation of this
profiles propagate and converge, the limiting s1tuat1on m which q/q 0 = c/c 0
is approached with the orofile a* /q 0 still Iaggmg. This reoresents a stable problem together with various possible s1rnplificatlons are summarized m
s1tuat1on smce there remains a finite dnvmg force for mass transfer but this 1s . I Table 2.10. Even if the equilibria are simple (e.g., 'linear or Langmu1r), the
the same at all concentration ievels. As a result this asymptotic profile will problem is far from trivial and the numerical computations are bulky. 1t is
propagate without any further change of shape. For obvious reasons this ts therefore essential to consider carefully the oo-ssibility of introctucmg appro-
referred to as "constant pattern" behavior. Thus, where equilibnum theory priate simplifying approx1mat1ons.
predicts a shock transition, 1n practice there will be a constant pattern front.
The distance required to approach the constant pattern depends on the
2.4.5 The LDF Rate Expression
extent of mass transfer resistance and the degree of axial mixmg m the
column. lf these effects are small; the constant pattern limit will be ar- In most adsorptton systems the kinetics are controlled mamlv by intrapart1cle
oroached rapidly, and tile resuitmg profile will be very sliarp, approaching diffusion, hut the use of a diffusion couat1on to model the kinetics introduces