Page 46 - Principles and Applications of NanoMEMS Physics

32 Chapter 1

However, unlike STM, no voltage is applied between the tip and the
sample. Instead of a tunneling current, the AFM detects the force elicited
between the tip and the sample. The tip is part of a force-sensing cantilever
beam so that, when the latter is raster-scanned over the sample, much like a
phonograph, surface height variations are detected by monitoring the
interference pattern produced by a laser beam reflecting off the cantilever
beam when the latter deflects/deforms.
The image of the sample is then extracted by relating the cantilever beam
deflection to the force required to produce it, F . F in turn, is related to
TS TS
the tip-sample (TS) potential V via its negative gradient,
TS
F = − ∂ V z ∂ and is characterized by an effective spring constant
TS TS
k = − ∂ F z ∂ . F may be attractive or repulsive, as it embodies a
TS TS TS
variety of forces, each one varying differently with TS distance z, thus
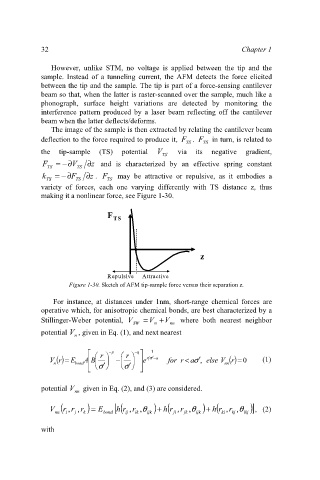
making it a nonlinear force, see Figure 1-30.

F F TS
TS

z z

Repulsive
Attractive
Repulsive Attractive
Figure 1-30. Sketch of AFM tip-sample force versus their separation z.
For instance, at distances under 1nm, short-range chemical forces are
operative which, for anisotropic chemical bonds, are best characterized by a
Stillinger-Weber potential, V SW = V + V where both nearest neighbor
n
nn
potential V , given in Eq. (1), and next nearest
n
ª § r · −p § r · −q º 1
V () = Er A « ¨ B ¸ − ¨ ¸ »e r σ − ′ a for r < aσ , ′ else V () 0=r (1)
n bond ¹ ′ σ ¹ ′ σ nn
« ¬ © © » ¼

potential V given in Eq. (2), and (3) are considered.
nn

V ( rr , r , ) E= h ( [ r , r θ , ) (rh+ , r θ , ) (rh+ , r θ , )], (2)
nn i j k bond ij ik ijk ji jk ijk ki kj ikj

with