Page 56 - Principles and Applications of NanoMEMS Physics

2. NANOMEMS PHYSICS: Quantum Wave-Particle Phenomena 43

m , and ε
t = 2 µ = 8 . 9 . Under these conditions of a metal stripe of
s r
relatively large dimensions with respect to a Bohr radius,
a 0=0.592ǖ=0.0592nm, the current I may be construed as consisting of an
ensemble of freely-propagating electrons, each characterized by a plane
wave-like wave function ψ ~ e , with continuous energy E = = 2 k 2 2m *,
ikz
where = is Planck’s constant, =k π 2 λ is the wave vector, λ the electron
wavelength, and m* the effective mass [58].
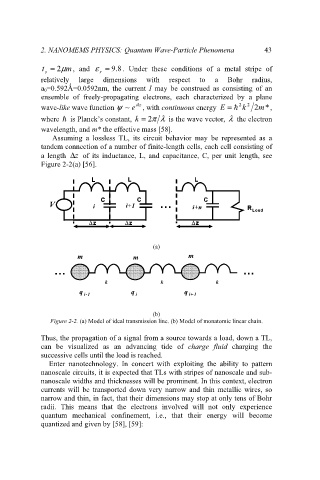
Assuming a lossless TL, its circuit behavior may be represented as a
tandem connection of a number of finite-length cells, each cell consisting of
a length z∆ of its inductance, L, and capacitance, C, per unit length, see
Figure 2-2(a) [56].
L L L L L L

C C C C C C
…
V V i i i+1 … i+n R R Load
i+1
i+n
Load
∆z
∆z ∆z ∆z
∆z
∆z
(a)
m m m m m m
… … …
…
k k k k k k
q q q q q q
i-1 i i i+ 1 1
i-1
i+
(b)
Figure 2-2. (a) Model of ideal transmission line. (b) Model of monatomic linear chain.

Thus, the propagation of a signal from a source towards a load, down a TL,
can be visualized as an advancing tide of charge fluid charging the
successive cells until the load is reached.
Enter nanotechnology. In concert with exploiting the ability to pattern
nanoscale circuits, it is expected that TLs with stripes of nanoscale and sub-
nanoscale widths and thicknesses will be prominent. In this context, electron
currents will be transported down very narrow and thin metallic wires, so
narrow and thin, in fact, that their dimensions may stop at only tens of Bohr
radii. This means that the electrons involved will not only experience
quantum mechanical confinement, i.e., that their energy will become
quantized and given by [58], [59]: