Page 177 - Probability and Statistical Inference

154 3. Multivariate Random Variables

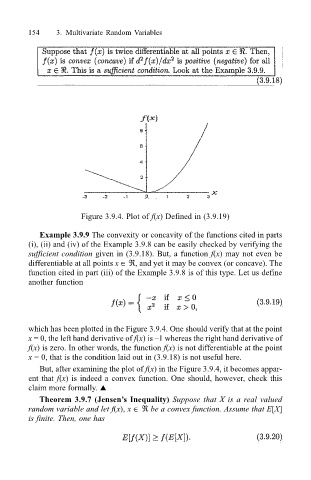
Figure 3.9.4. Plot of f(x) Defined in (3.9.19)

Example 3.9.9 The convexity or concavity of the functions cited in parts
(i), (ii) and (iv) of the Example 3.9.8 can be easily checked by verifying the
sufficient condition given in (3.9.18). But, a function f(x) may not even be
differentiable at all points x ∈ ℜ, and yet it may be convex (or concave). The
function cited in part (iii) of the Example 3.9.8 is of this type. Let us define
another function

which has been plotted in the Figure 3.9.4. One should verify that at the point
x = 0, the left hand derivative of f(x) is –1 whereas the right hand derivative of
f(x) is zero. In other words, the function f(x) is not differentiable at the point
x = 0, that is the condition laid out in (3.9.18) is not useful here.
But, after examining the plot of f(x) in the Figure 3.9.4, it becomes appar-
ent that f(x) is indeed a convex function. One should, however, check this
claim more formally. !
Theorem 3.9.7 (Jensen’s Inequality) Suppose that X is a real valued
random variable and let f(x), x ∈ ℜ be a convex function. Assume that E[X]
is finite. Then, one has