Page 281 - Probability and Statistical Inference

258 5. Concepts of Stochastic Convergence

version of the sample mean of iid real valued random variables having a
positive and finite variance.
Theorem 5.3.4 (Central Limit Theorem) Let X , ..., X be iid real val-
n
1
2
ued random variables having the common mean µ and variance σ , –∞ < µ <
∞ and 0 < σ < ∞. Then, as n → ∞, we have

A careful treatment of the proof of the CLT under such generality requires
working knowledge of the characteristic functions and hence it is out of
scope of this book. The reader may look at Sen and Singer (1993, pp. 107-
108) for a proof of this result and other versions of the CLT.
If one however assumes additionally that the mgf of X exists, then a proof
1
of the CLT can be constructed fairly easily, essentially along the lines of the
Examples 5.3.3-5.3.4. The details are left out as the Exercise 5.3.3.

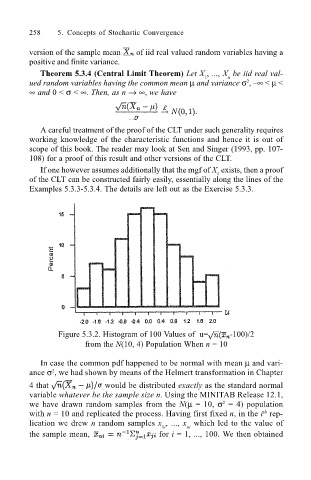
Figure 5.3.2. Histogram of 100 Values of u= -100)/2
from the N(10, 4) Population When n = 10

In case the common pdf happened to be normal with mean µ and vari-
ance σ , we had shown by means of the Helmert transformation in Chapter
2
4 that would be distributed exactly as the standard normal
variable whatever be the sample size n. Using the MINITAB Release 12.1,
2
we have drawn random samples from the N(µ = 10, σ = 4) population
with n = 10 and replicated the process. Having first fixed n, in the i rep-
th
lication we drew n random samples x , ..., x which led to the value of
1i ni
the sample mean, for i = 1, ..., 100. We then obtained