Page 427 - Probability and Statistical Inference
P. 427
404 8. Tests of Hypotheses
α. See the Examples 8.3.6-8.3.7.
A final form of the MP or UMP level a test is written down in the
simplest implementable form. That is, having fixed α ∈ (0, 1), the
c
cut-off point of the test defining the regions R, R must explicitly
be found analytically or from a standard statistical table.
Remark 8.3.3 We note that, for all practical purposes, the MP level α test
given by the Neyman-Pearson Lemma is unique. In other words, if one finds
another MP level α test with its test function ψ* by some other method, then
for all practical purposes, ψ* and ψ will coincide on the two sets {X ∈ χ :
n
L(x; θ ) > kL(x; θ )} and {x ∈ χ : L(x; θ ) < kL(x; θ )}.
n
1 0 1 0
Convention: k is used as a generic and nonstochastic constant.
k may not remain same from one step to another.
Example 8.3.1 Let X , ..., X be iid N(µ, σ ) with unknown µ ∈ ℜ, but
2
n
1
assume that σ ∈ ℜ + is known. With preassigned α ∈ (0, 1) we wish to
derive the MP level α test for H : µ = µ versus H : µ = µ where µ > µ and
0 0 1 1 1 0
µ , µ are two known real numbers. Both H , H are simple hypotheses and
1
0
0
1
the Neyman-Pearson Lemma applies. The likelihood function is given by
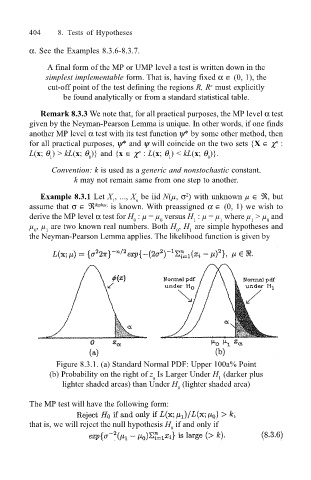
Figure 8.3.1. (a) Standard Normal PDF: Upper 100a% Point
(b) Probability on the right of z Is Larger Under H (darker plus
1
a
lighter shaded areas) than Under H (lighter shaded area)
0
The MP test will have the following form:
that is, we will reject the null hypothesis H if and only if
0