Page 223 - Process Modelling and Simulation With Finite Element Methods

21 0 Process Modelling and Simulation with Finite Element Methods

step to time step, but the average growth of power in all Fourier modes with the
same wavenumber was exponential and agreed well with the linear stability
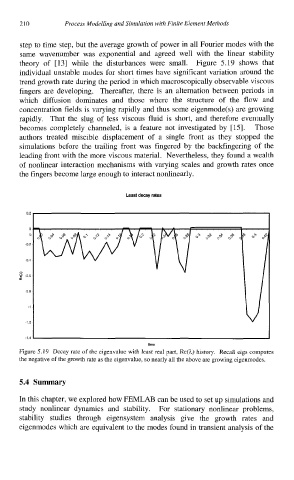
theory of [13] while the disturbances were small. Figure 5.19 shows that
individual unstable modes for short times have significant variation around the
trend growth rate during the period in which macroscopically observable viscous
fingers are developing. Thereafter, there is an alternation between periods in
which diffusion dominates and those where the structure of the flow and
concentration fields is varying rapidly and thus some eigenmode( s) are growing
rapidly. That the slug of less viscous fluid is short, and therefore eventually
becomes completely channeled, is a feature not investigated by [15]. Those
authors treated miscible displacement of a single front as they stopped the
simulations before the trailing front was fingered by the backfingering of the
leading front with the more viscous material. Nevertheless, they found a wealth
of nonlinear interaction mechanisms with varying scales and growth rates once
the fingers become large enough to interact nonlinearly.

Least decay rates

time
Figure 5.19 Decay rate of the eigenvalue with least real part, Re(l.) history. Recall eigs computes
the negative of the growth rate as the eigenvalue, so nearly all the above are growing eigenmodes.

5.4 Summary

In this chapter, we explored how FEMLAB can be used to set up simulations and
study nonlinear dynamics and stability. For stationary nonlinear problems,
stability studies through eigensystem analysis give the growth rates and
eigenmodes which are equivalent to the modes found in transient analysis of the