Page 317 - Process Modelling and Simulation With Finite Element Methods

304 Process Modelling and Simulation with Finite Element Methods

120

100
-
5 flo
:
a 60
m
d 40
20
0
0 05 1 15 2 25
Time
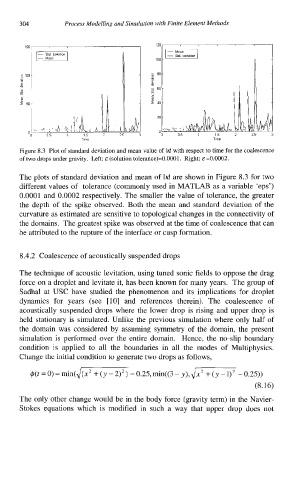
Figure 8.3 Plot of standard deviation and mean value of Id with respect to time for the coalescence
of two drops under gravity. Left: E (solution tolerance)=0.0001. Right: E =0.0002.

The plots of standard deviation and mean of Id are shown in Figure 8.3 for two
different values of tolerance (commonly used in MATLAB as a variable ‘eps’)
0.0001 and 0.0002 respectively. The smaller the value of tolerance, the greater
the depth of the spike observed. Both the mean and standard deviation of the
curvature as estimated are sensitive to topological changes in the connectivity of
the domains. The greatest spike was observed at the time of coalescence that can
be attributed to the rupture of the interface or cusp formation.

8.4.2 Coalescence of acoustically suspended drops

The technique of acoustic levitation, using tuned sonic fields to oppose the drag
force on a droplet and levitate it, has been known for many years. The group of
Sadhal at USC have studied the phenomenon and its implications for droplet
dynamics for years (see [lo] and references therein). The coalescence of
acoustically suspended drops where the lower drop is rising and upper drop is
held stationary is simulated. Unlike the previous simulation where only half of
the domain was considered by assuming symmetry of the domain, the present
simulation is performed over the entire domain. Hence, the no-slip boundary
condition is applied to all the boundaries in all the modes of Multiphysics.
Change the initial condition to generate two drops as follows,

-
- 0.25, min((3 - y), 4
$(t = 0) = min(4- - 0.25))
(8.16)
The only other change would be in the body force (gravity term) in the Navier-
Stokes equations which is modified in such a way that upper drop does not