Page 17 - Radar Technology Encyclopedia

accuracy of sequential lobing, fundamental acquisition, reacquisition 7

2
sinx/x beam
Gaussian
AGC
beam
Target
1.5 Receiver boxcar t , t + present
Normalized error slope 1 2-way S Threshold S boxcar t , t * a
Peak
1
2
Gate
Area
1
2
Gate
0.5 1-way Acquisition gate t
t
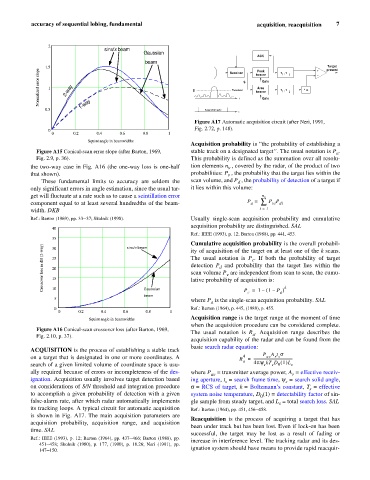
Figure A17 Automatic acquisition circuit (after Neri, 1991,
0 Fig. 2.72, p. 148).
0 0.2 0.4 0.6 0.8 1
Squint angle in beamwidths
Acquisition probability is “the probability of establishing a
Figure A15 Conical-scan error slope (after Barton, 1969, stable track on a designated target”. The usual notation is P .
a
Fig. 2.9, p. 36). This probability is defined as the summation over all resolu-
the two-way case in Fig. A16 (the one-way loss is one-half tion elements n , covered by the radar, of the product of two
v
that shown). probabilities: P , the probability that the target lies within the
v
These fundamental limits to accuracy are seldom the scan volume, and P , the probability of detection of a target if
d
only significant errors in angle estimation, since the usual tar- it lies within this volume:
get will fluctuate at a rate such as to cause a scintillation error n v
a å
component equal to at least several hundredths of the beam- P = P P
vi di
width. DKB i = 1
Ref.: Barton (1969), pp. 33–37; Skolnik (1990). Usually single-scan acquisition probability and cumulative
acquisition probability are distinguished. SAL
40
Ref.: IEEE (1993), p. 12; Barton (1988), pp. 441, 453.
35
Cumulative acquisition probability is the overall probabil-
Crossover loss in dB (2-way) 25 The usual notation is P . If both the probability of target
sinx/x beam
30
ity of acquisition of the target on at least one of the k scans.
c
detection P and probability that the target lies within the
d
20
scan volume P are independent from scan to scan, the cumu-
v
15
lative probability of acquisition is:
k
Gaussian
10
a
c
beam P = 1 – ( 1 – P )
5 where P is the single-scan acquisition probability. SAL
a
0 Ref.: Barton (1964), p. 445, (1988), p. 455.
0 0.2 0.4 0.6 0.8 1
Squint angle in beamwidths Acquisition range is the target range at the moment of time
when the acquisition procedure can be considered complete.
Figure A16 Conical-scan crossover loss (after Barton, 1969,
The usual notation is R . Acquisition range describes the
Fig. 2.10, p. 37). a
acquisition capability of the radar and can be found from the
basic search radar equation:
ACQUISITION is the process of establishing a stable track
P A t s
4
on a target that is designated in one or more coordinates. A R = -------------------------------------------
av r s
a
search of a given limited volume of coordinate space is usu- 4pykT D 1 () L s
0
s
s
ally required because of errors or incompleteness of the des- where P = transmitter average power, A = effective receiv-
av r
ignation. Acquisition usually involves target detection based ing aperture, t = search frame time, y = search solid angle,
s s
on considerations of S/N threshold and integration procedure s= RCS of target, k = Boltzmann’s constant, T = effective
s
to accomplish a given probability of detection with a given system noise temperature, D (1) = detectability factor of sin-
0
false-alarm rate, after which radar automatically implements gle sample from steady target, and L = total search loss. SAL
s
its tracking loops. A typical circuit for automatic acquisition Ref.: Barton (1964), pp. 451, 456–458.
is shown in Fig. A17. The main acquisition parameters are
Reacquisition is the process of acquiring a target that has
acquisition probability, acquisition range, and acquisition
been under track but has been lost. Even if lock-on has been
time. SAL
successful, the target may be lost as a result of fading or
Ref.: IEEE (1993), p. 12; Barton (1964), pp. 437–466; Barton (1988), pp.
increase in interference level. The tracking radar and its des-
451–458; Skolnik (1980), p. 177, (1990), p. 18.26; Neri (1991), pp.
147–150. ignation system should have means to provide rapid reacquir-