Page 16 - Radar Technology Encyclopedia

6 accuracy of radar measurement, fundamental accuracy of sequential lobing, fundamental

estimated angle, the higher the angular measurement accu- get, is limited by thermal noise, and is measured by the ran-
racy. SAL dom noise error component s q :
Ref.: Skolnik (1980), pp. 400–411; Shirman (1981), pp. 200–205; Leonov q 3
(1988), p. 25. s = -----------------------------
q
¤
(
k 2 EN )
0
The fundamental accuracy of monopulse is achieved by
comparison of signal amplitudes in beams formed simulta- where q is the one-way half-power beamwidth, k is a pattern
3
neously (monopulse estimation or simultaneous lobing) per- slope constant, and E/N is the applicable signal-to-noise
0
mits the radar to approach the fundamental accuracy limit energy ratio. The different scanning options lead to different
given by values of k and E/N .
0
For the case of continuous (linear or sector) scanning, the
q 3
s = --------------------------------- slope constant becomes k = 1.66 and the energy ratio is that
q p
(
¤
k 2 EN )
m 0 of n pulses received with the on-axis ratio (S/N) divided by a
m
where k @ 1.6 is the monopulse slope constant and E/ beamshape loss, L = 1.33.
p
m
N =2n(S/N) is the total energy ratio for a target on the sum For a step-scanned beam, the slope constant is given by
m
0
beam axis. When the target is displaced from the axis, the dG ¤( G )
df
2
1
error will increase for two reasons: (a) the energy ratio in the k = --------------------- = --------------------------
(
¤
(
¤
sum channel will decrease, and (b) a second component of d qq ) d qq )
3
3
error, caused by noise in the normalization process (by which
where f is the voltage pattern of the beam, and G and G are
1
2
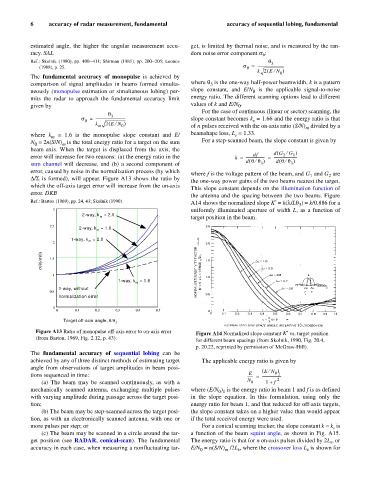
D/S is formed), will appear. Figure A13 shows the ratio by
the one-way power gains of the two beams nearest the target.
which the off-axis target error will increase from the on-axis
This slope constant depends on the illumination function of
error. DKB
the antenna and the spacing between the two beams. Figure
Ref.: Barton (1969), pp. 24, 43; Skolnik (1990). A14 shows the normalized slope K¢ = k(l/Lq ) = k/0.886 for a
3
3 uniformly illuminated aperture of width L, as a function of
2-way, k = 2.0 target position in the beam.
m
2.5
2-way, k = 1.6
m
1-way, k = 2.0
s(q)/s(0) 1.5 2 m
1
1-way, k = 1.6
m
1-way, without
0.5
normalization error
0
0 0.1 0.2 0.3 0.4 0.5
Target off-axis angle, q/q
3
Figure A13 Ratio of monopulse off-axis error to on-axis error Figure A14 Normalized slope constant K¢ vs. target position
(from Barton, 1969, Fig. 2.12, p. 43).
for different beam spacings (from Skolnik, 1990, Fig. 20.4,
p. 20.22, reprinted by permission of McGraw-Hill).
The fundamental accuracy of sequential lobing can be
achieved by any of three distinct methods of estimating target The applicable energy ratio is given by
angle from observations of target amplitudes in beam posi- ( EN )
¤
E
0 1
tions sequenced in time: ------ = ---------------------
2
(a) The beam may be scanned continuously, as with a N 0 1 + f
mechanically scanned antenna, exchanging multiple pulses where (E/N ) is the energy ratio in beam 1 and f is as defined
0 1
with varying amplitude during passage across the target posi- in the slope equation. In this formulation, using only the
tion; energy ratio for beam 1, and that reduced for off-axis targets,
(b) The beam may be step-scanned across the target posi- the slope constant takes on a higher value than would appear
tion, as with an electronically scanned antenna, with one or if the total received energy were used.
more pulses per step; or For a conical scanning tracker, the slope constant k = k is
s
(c) The beam may be scanned in a circle around the tar- a function of the beam squint angle, as shown in Fig. A15.
get position (see RADAR, conical-scan). The fundamental The energy ratio is that for n on-axis pulses divided by 2L , or
k
accuracy in each case, when measuring a nonfluctuating tar- E/N = n(S/N) /2L , where the crossover loss L is shown for
0
m
k
k