Page 102 - Radiochemistry and nuclear chemistry

Unstable Nuclei and Radioactive Decay 91

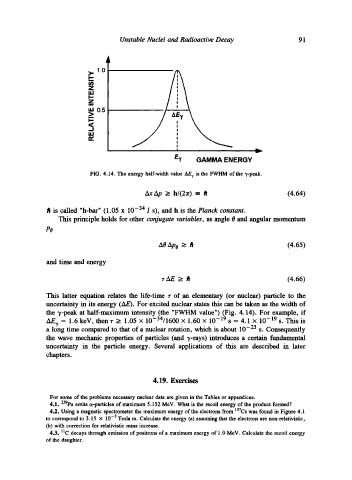
>.. 1.0
I--
Z
Ill
I'--
Z
U.I 0.5
>

Ir
IZ

E1 GAMMA ENERGY
FIG. 4.14. The energy half-width value AE~ is the FWHM of the 7-peak.

~:Ap > h/(2~') - (4.64)

fl is called "h-bar" (1.05 x 10 -34 J s), and h is the Planck constant.
This principle holds for other conjugate variables, as angle 0 and angular momentum
PO

AO APo >_ ~ (4.65)

and time and energy

7"AE _ h (4.66)

This latter equation relates the life-time r of an elementary (or nuclear) particle to the
uncertainty in its energy (AE). For excited nuclear states this can be taken as the width of
the v-peak at half-maximum intensity (the "FWHM value') (Fig. 4.14). For example, if
AE./= 1.6 keV, then ~- > 1.05 x 10-34/1600 x 1.60 x 10 -19 s = 4.1 x 10 -19 s. This is
a long time compared to that of a nuclear rotation, which is about 10 -23 s. Consequently
the wave mechanic properties of particles (and v-rays) introduces a certain fundamental
uncertainty in the particle energy. Several applications of this are described in later
chapters.

4.19. Exercises

For some of the problems necessary nuclear data are given in the Tables or appendices.
4.1. ~gPu emits s-particles of maximum 5.152 MeV. What is the recoil energy of the product formed?
4.2. Using a magnetic spectrometer the maximum energy of the electrons from 137Cs was found in Figure 4.1
to correspond to 3.15 x 10 -3 Tesla m. Calculate the energy (a) assuming that the electrons are non-relativistic,
(b) with correction for relativistic mass increase.
4.3. llC decays through emission of positrons of a maximum energy of 1.0 MeV. Calculate the recoil energy
of the daughter.