Page 99 - Radiochemistry and nuclear chemistry

88 Radiochemistry and Nuclear Chemistry

At t .~ tth, 1 (t ~ 12.8 d) the first exponential term is very close to 1 and A 2 increases
proportional to (1 - e-O'693t/t,,t,2); this is the increasing part of curve (2). At t ~, t1~,2 (t
40 h), the second exponential term becomes much smaller than the first one, and A 2
decreases proportional to e-~ For this part of the curve we may write

N2 = N1 )~1 /()~2 -- )~1) (4.58)

which is the relation valid for transient equilibrium. The total activity of the barium sample,
curve (3), is the sum of curves (1) and (2).
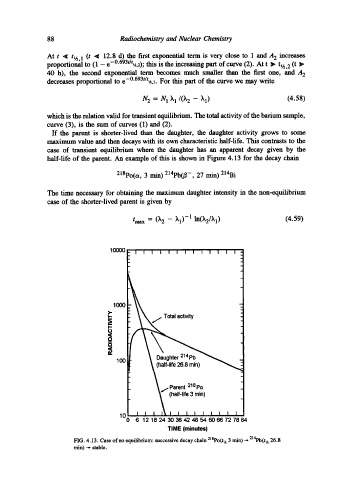
If the parent is shorter-lived than the daughter, the daughter activity grows to some
maximum value and then decays with its own characteristic half-life. This contrasts to the
case of transient equilibrium where the daughter has an apparent dexay given by the
half-life of the parent. An example of this is shown in Figure 4.13 for the decay chain
218po(ct, 3 rain)214pb(~-, 27 rain)214Bi

The time necessary for obtaining the maximum daughter intensity in the non-equilibrium
case of the shorter-lived parent is given by

/max = (k2 -- ~1 )-1 ln(~2/~l) (4.59)

'1
10000 I I I I I I I I I I I I I

1000
Total activity
m
i--
o

100 Daughter 214 Pb
(half-life 26.8 rain)

Parent 218 Po
(half-life 3 rain)

2
100 6 I 18 24 30 36 42 48 54 60 66 72 78 84
TIME (minutes)
FIG. 4.13. Case of no equilibrium: successive decay chain 21SPo(t,~ 3 min)--- 2141~(t,~ 26.8
rain) --- stable.