Page 68 - Rapid Learning in Robotics

54 The PSOM Algorithm

following an error-minimization process. This is particularly useful to im-
prove the a PSOM that was constructed with a noisy sampled training set
or to adapt it to a changing or drifting system.
In the following we propose a supervised learning rule for the refer-
ence vectors w a , minimizing the obtained output error. Required is the
target, the embedded input–output vector, here also denoted x. The best-

match w s M for the current input x is found according to the cur-
rent input sub-space specification (set of components I; distance metric P).
Each reference vector is then adjusted, weighted by its contribution factor
H , minimizing the deviation to the desired joint input-output vector x

w a a s x H w s (4.14)

1 after training
reference vectors W_a
training data set
0.8 before training

0.6

0.4

0.2

0

-1 -0.5 0 0.5 1

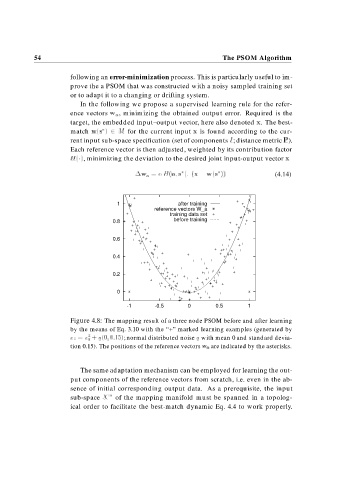
Figure 4.8: The mapping result of a three node PSOM before and after learning
by the means of Eq. 3.10 with the “+” marked learning examples (generated by

x x ; normal distributed noise with mean 0 and standard devia-

tion 0.15). The positions of the reference vectors w a are indicated by the asterisks.

The same adaptation mechanism can be employed for learning the out-
put components of the reference vectors from scratch, i.e. even in the ab-
sence of initial corresponding output data. As a prerequisite, the input
sub-space X in of the mapping manifold must be spanned in a topolog-
ical order to facilitate the best-match dynamic Eq. 4.4 to work properly.