Page 111 - Reservoir Geomechanics

95 Rock failure in compression, tension and shear

a. 500 b. 500
450 450
400 400
s = 90 MPa
3
350 350
s = 90 MPa
3
300 300 s = 60 MPa
3
s 1 (MPa) 250 s = 60 MPa s 1 (MPa) 250 s 1 = s 2
3
200 s 1 = s 2 200 s = 30 MPa
3
150 s = 30 MPa 150
3
Hoek and Brown criterion
100 Mohr Coulomb criterion 100 C = 60 MPa
0
C = 60 MPa m = 16
0
50 s = 0 MPa m = 0.6 50 s = 0 MPa s = 1
3
3
i
0 0
0 50 100 150 200 250 300 350 400 450 500 0 50 100 150 200 250 300 350 400 450 500
s (MPa) s (MPa)
2 2
c. 500 d. 500
450 450
400 s = 90 MPa 400
3
350 350 s = 90 MPa
3
300 s = 60 MPa 300
s 1 (MPa) 250 s 1 = s 2 3 s 1 (MPa) 250 s = 60 MPa
3
200 200 s 1 = s 2
s = 30 MPa
3 s = 30 MPa
150 150 3
100 Modified Lade criterion 100 Modified Wiebols and Cook criterion
s = 0 MPa s = 0 MPa
3
0
50 3 C = 60 MPa 50 C = 60 MPa
0
m = 0.6 m = 0.6
i
i
0 0
0 50 100 150 200 250 300 350 400 450 500 0 50 100 150 200 250 300 350 400 450 500
s (MPa) s (MPa)
2 2
e. 500
450
s = 30 MPa
3
400
350
300
s 1 (MPa) 250 s 1 = s 2
200 s = 0 MPa
3
150 s = 30 MPa
3
100 Inscribed Drucker–Prager criterion
Circumscribed Drucker–Prager criterion
0
50 s = 0 MPa C = 60 MPa
3
m = 0.6
i
0
0 50 100 150 200 250 300 350 400 450 500
s (MPa)
2
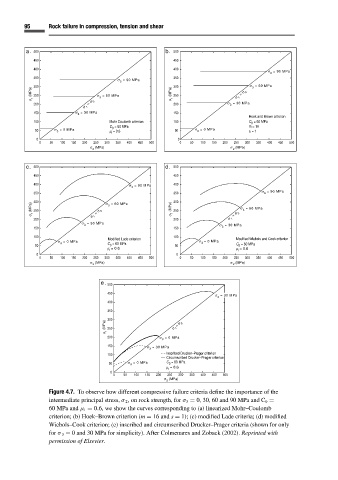
Figure 4.7. To observe how different compressive failure criteria define the importance of the
intermediate principal stress, σ 2 ,on rock strength, for σ 3 = 0, 30, 60 and 90 MPa and C 0 =
60 MPa and µ i = 0.6, we show the curves corresponding to (a) linearized Mohr–Coulomb
criterion; (b) Hoek–Brown criterion (m = 16 and s = 1); (c) modified Lade criteria; (d) modified
Wiebols–Cook criterion; (e) inscribed and circumscribed Drucker–Prager criteria (shown for only
for σ 3 = 0 and 30 MPa for simplicity). After Colmenares and Zoback (2002). Reprinted with
permission of Elsevier.