Page 108 - Reservoir Geomechanics

92 Reservoir geomechanics

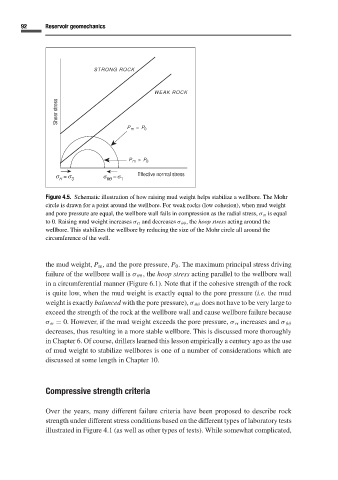
STRONG ROCK

WEAK ROCK
Shear stress

P = P 0
m

P > P 0
m
s = s s = s Effective normal stress
rr 3 qq 1

Figure 4.5. Schematic illustration of how raising mud weight helps stabilize a wellbore. The Mohr
circle is drawn for a point around the wellbore. For weak rocks (low cohesion), when mud weight
and pore pressure are equal, the wellbore wall fails in compression as the radial stress, σ rr is equal
to 0. Raising mud weight increases σ rr and decreases σ θθ , the hoop stress acting around the
wellbore. This stabilizes the wellbore by reducing the size of the Mohr circle all around the
circumference of the well.

the mud weight, P m , and the pore pressure, P 0 . The maximum principal stress driving
failure of the wellbore wall is σ θθ , the hoop stress acting parallel to the wellbore wall
in a circumferential manner (Figure 6.1). Note that if the cohesive strength of the rock
is quite low, when the mud weight is exactly equal to the pore pressure (i.e. the mud
weight is exactly balanced with the pore pressure), σ θθ does not have to be very large to
exceed the strength of the rock at the wellbore wall and cause wellbore failure because

σ rr = 0. However, if the mud weight exceeds the pore pressure, σ rr increases and σ θθ
decreases, thus resulting in a more stable wellbore. This is discussed more thoroughly
in Chapter 6.Of course, drillers learned this lesson empirically a century ago as the use
of mud weight to stabilize wellbores is one of a number of considerations which are
discussed at some length in Chapter 10.

Compressive strength criteria

Over the years, many different failure criteria have been proposed to describe rock
strength under different stress conditions based on the different types of laboratory tests
illustrated in Figure 4.1 (as well as other types of tests). While somewhat complicated,