Page 139 - Reservoir Geomechanics

122 Reservoir geomechanics

300

250
f

200
Pressure – S 3 (psi) 150 L

100
VERY STRONG SANDSTONE, DOLOMITE

50
WEAK SANDSTONE
0
0 0.2 0.4 0.6 0.8 1.0
Fracture length (meters)

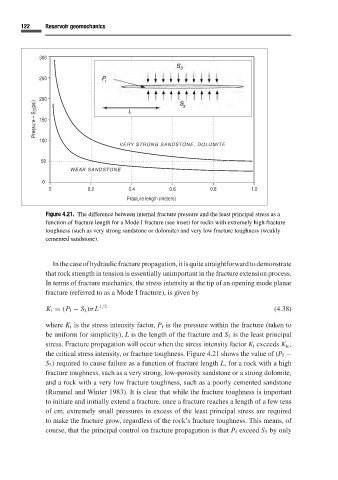
Figure 4.21. The difference between internal fracture pressure and the least principal stress as a
function of fracture length for a Mode I fracture (see inset) for rocks with extremely high fracture
toughness (such as very strong sandstone or dolomite) and very low fracture toughness (weakly
cemented sandstone).

Inthecaseofhydraulicfracturepropagation,itisquitestraightforwardtodemonstrate
that rock strength in tension is essentially unimportant in the fracture extension process.
In terms of fracture mechanics, the stress intensity at the tip of an opening mode planar
fracture (referred to as a Mode I fracture), is given by

K i = (P f − S 3 )π L 1/2 (4.38)

where K i is the stress intensity factor, P f is the pressure within the fracture (taken to
be uniform for simplicity), L is the length of the fracture and S 3 is the least principal
stress. Fracture propagation will occur when the stress intensity factor K i exceeds K ic ,
the critical stress intensity, or fracture toughness. Figure 4.21 shows the value of (P f −
S 3 ) required to cause failure as a function of fracture length L, for a rock with a high
fracture toughness, such as a very strong, low-porosity sandstone or a strong dolomite,
and a rock with a very low fracture toughness, such as a poorly cemented sandstone
(Rummel and Winter 1983). It is clear that while the fracture toughness is important
to initiate and initially extend a fracture, once a fracture reaches a length of a few tens
of cm, extremely small pressures in excess of the least principal stress are required
to make the fracture grow, regardless of the rock’s fracture toughness. This means, of
course, that the principal control on fracture propagation is that P f exceed S 3 by only