Page 153 - Reservoir Geomechanics

136 Reservoir geomechanics

m i
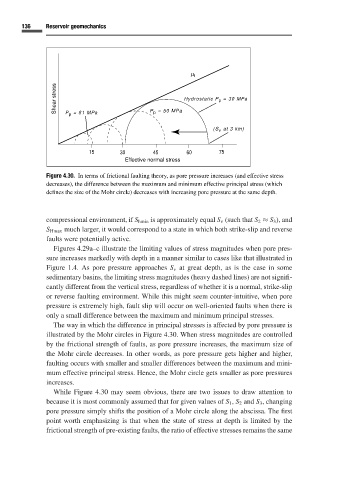
Shear stress P p = 81 MPa P = 50 MPa Hydrostatic P = 30 MPa

p
p

(S at 3 km)
v

15 30 45 60 75
Effective normal stress

Figure 4.30. In terms of frictional faulting theory, as pore pressure increases (and effective stress
decreases), the difference between the maximum and minimum effective principal stress (which
defines the size of the Mohr circle) decreases with increasing pore pressure at the same depth.

compressional environment, if S hmin is approximately equal S v (such that S 2 ≈ S 3 ), and
S Hmax much larger, it would correspond to a state in which both strike-slip and reverse
faults were potentially active.
Figures 4.29a–c illustrate the limiting values of stress magnitudes when pore pres-
sure increases markedly with depth in a manner similar to cases like that illustrated in
Figure 1.4.As pore pressure approaches S v at great depth, as is the case in some
sedimentary basins, the limiting stress magnitudes (heavy dashed lines) are not signifi-
cantly different from the vertical stress, regardless of whether it is a normal, strike-slip
or reverse faulting environment. While this might seem counter-intuitive, when pore
pressure is extremely high, fault slip will occur on well-oriented faults when there is
only a small difference between the maximum and minimum principal stresses.
The way in which the difference in principal stresses is affected by pore pressure is
illustrated by the Mohr circles in Figure 4.30. When stress magnitudes are controlled
by the frictional strength of faults, as pore pressure increases, the maximum size of
the Mohr circle decreases. In other words, as pore pressure gets higher and higher,
faulting occurs with smaller and smaller differences between the maximum and mini-
mum effective principal stress. Hence, the Mohr circle gets smaller as pore pressures
increases.
While Figure 4.30 may seem obvious, there are two issues to draw attention to
because it is most commonly assumed that for given values of S 1 , S 2 and S 3 , changing
pore pressure simply shifts the position of a Mohr circle along the abscissa. The first
point worth emphasizing is that when the state of stress at depth is limited by the
frictional strength of pre-existing faults, the ratio of effective stresses remains the same