Page 62 - Reservoir Geomechanics

46 Reservoir geomechanics

0.4
j = 0.386
0

0.35

0.3

Shale porosity 0.25 j = j e -bs v

0.2 0
-1
-2
(b = 3.13 × 10 MPa )
.
0.15

0.1
0 10 20 30 40 50
Effective vertical stress (MPa)
l = 0.44
p
1 2 3 km
l = 0.65
p
1 2 3 4 5 6
l = 0.8
p
1 2 3 4 5 6 7 8 9 10
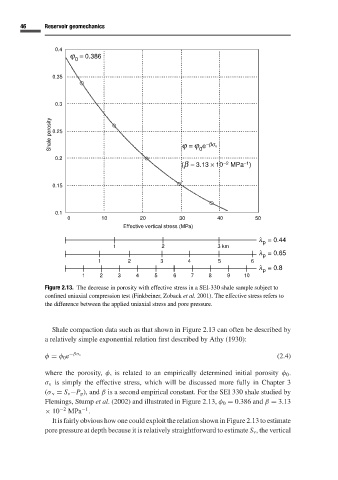
Figure 2.13. The decrease in porosity with effective stress in a SEI-330 shale sample subject to
confined uniaxial compression test (Finkbeiner, Zoback et al. 2001). The effective stress refers to
the difference between the applied uniaxial stress and pore pressure.

Shale compaction data such as that shown in Figure 2.13 can often be described by
a relatively simple exponential relation first described by Athy (1930):

φ = φ 0 e −βσ v (2.4)

where the porosity, φ,is related to an empirically determined initial porosity φ 0 .
σ v is simply the effective stress, which will be discussed more fully in Chapter 3
(σ v = S v −P p ), and β is a second empirical constant. For the SEI 330 shale studied by
Flemings, Stump et al.(2002) and illustrated in Figure 2.13, φ 0 = 0.386 and β = 3.13
−1
× 10 −2 MPa .
It is fairly obvious how one could exploit the relation shown in Figure 2.13 to estimate
pore pressure at depth because it is relatively straightforward to estimate S v , the vertical