Page 108 - Schaum's Outline of Theory and Problems of Advanced Calculus

CHAP. 5] INTEGRALS 99

Fig. 5-3

ARC LENGTH
As you walk a twisting mountain trail, it is possible to determine the distance covered by using a
pedometer. To create a geometric model of this event, it is necessary to describe the trail and a method
of measuring distance along it. The trail might be referred to as a path, but in more exacting geometric
terminology the word, curve is appropriate. That segment to be measured is an arc of the curve. The
arc is subject to the following restrictions:

1. It does not intersect itself (i.e., it is a simple arc).
2. There is a tangent line at each point.
3. The tangent line varies continuously over the arc.
These conditions are satisfied with a parametric representation x ¼ f ðtÞ; y ¼ gðtÞ; z ¼ hðtÞ; a @ t @ b,
where the functions f , g,and h have continuous derivatives that do not simultaneously vanish at any
point. This arc is in Euclidean three space and will be discussed in Chapter 10. In this introduction to
curves and their arc length, we let z ¼ 0, thereby restricting the discussion to the plane.
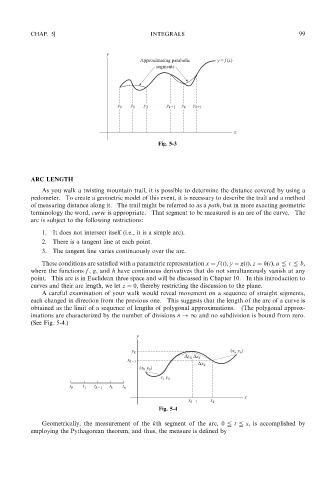
A careful examination of your walk would reveal movement on a sequence of straight segments,
each changed in direction from the previous one. This suggests that the length of the arc of a curve is
obtained as the limit of a sequence of lengths of polygonal approximations. (The polygonal approx-
imations are characterized by the number of divisions n !1 and no subdivision is bound from zero.
(See Fig. 5-4.)

Fig. 5-4
Geometrically, the measurement of the kth segment of the arc, 0 @ t @ s,is accomplished by
employing the Pythagorean theorem, and thus, the measure is defined by