Page 153 - Schaum's Outline of Theory and Problems of Electric Circuits

FIRST-ORDER CIRCUITS
142
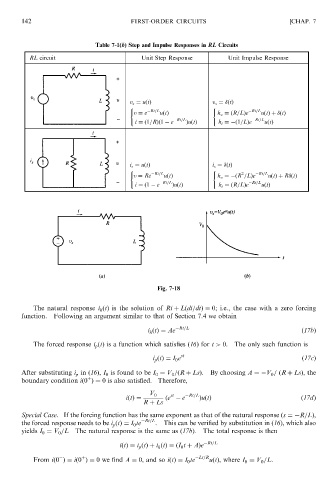
Table 7-1(b) Step and Impulse Responses in RL Circuits [CHAP. 7
RL circuit Unit Step Response Unit Impulse Response

v s ¼ uðtÞ v s ¼ ðtÞ
( (
v ¼ e Rt=L uðtÞ h v ¼ðR=LÞe Rt=L uðtÞþ ðtÞ
i ¼ð1=RÞð1 e Rt=L ÞuðtÞ h i ¼ ð1=LÞe Rt=L uðtÞ

i s ¼ uðtÞ i s ¼ ðtÞ
( (
2
v ¼ Re Rt=L uðtÞ h v ¼ ðR =LÞe Rt=L uðtÞþ R ðtÞ
i ¼ð1 e Rt=L ÞuðtÞ h i ¼ðR=LÞe Rt=L uðtÞ

Fig. 7-18

The natural response i h ðtÞ is the solution of Ri þ Lðdi=dtÞ¼ 0; i.e., the case with a zero forcing
function. Following an argument similar to that of Section 7.4 we obtain
Rt=L
i h ðtÞ¼ Ae ð17bÞ

The forced response i p ðtÞ is a function which satisfies (16) for t > 0. The only such function is
i p ðtÞ¼ I 0 e st ð17cÞ

After substituting i in (16), I is found to be I ¼ V =ðR þ LsÞ. By choosing A ¼ V = ðR þ LsÞ, the
p
0
0
0
0
þ
boundary condition ið0 Þ¼ 0 is also satisfied. Therefore,
V 0 st Rt=L
iðtÞ¼ ðe e ÞuðtÞ ð17dÞ
R þ Ls
Special Case. If the forcing function has the same exponent as that of the natural response ðs ¼ R=LÞ,
Rt=L
the forced response needs to be i ðtÞ¼ I te . This can be verified by substitution in (16), which also
p
0
yields I 0 ¼ V 0 =L The natural response is the same as (17b). The total response is then
Rt=L
iðtÞ¼ i p ðtÞþ i h ðtÞ¼ðI 0 t þ AÞe

þ
From ið0 Þ¼ ið0 Þ¼ 0 we find A ¼ 0, and so iðtÞ¼ I 0 te Lt=R uðtÞ, where I 0 ¼ V 0 =L.