Page 204 - Schaum's Outline of Theory and Problems of Electric Circuits

SINUSOIDAL STEADY-STATE CIRCUIT ANALYSIS
CHAP. 9]
Equating coefficients of like terms in (1) and (2), 193

V sin ¼ !LI and V cos ¼ RI
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
Then v ¼ I R þð!LÞ sin ½!t þ arctan ð!L=Rފ
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
and V ¼ I R þð!LÞ 2 and ¼ tan 1 !L
R
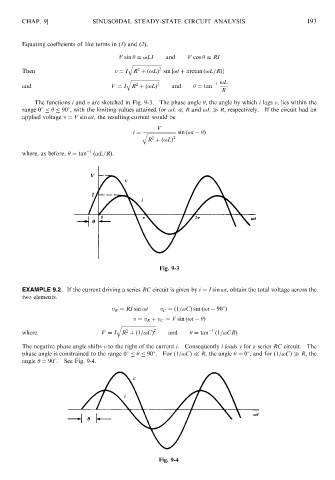
The functions i and v are sketched in Fig. 9-3. The phase angle , the angle by which i lags v, lies within the
range 08 908, with the limiting values attained for !L R and !L R, respectively. If the circuit had an
applied voltage v ¼ V sin !t, the resulting current would be
V
i ¼ q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi sin ð!t Þ
2
R þð!LÞ 2
where, as before, ¼ tan 1 ð!L=RÞ.

Fig. 9-3

EXAMPLE 9.2 If the current driving a series RC circuit is given by i ¼ I sin !t, obtain the total voltage across the
two elements.
v R ¼ RI sin !t v C ¼ð1=!CÞ sin ð!t 908Þ
v ¼ v R þ v C ¼ V sin ð!t Þ
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
where V ¼ I R þð1=!CÞ 2 and ¼ tan 1 ð1=!CRÞ
The negative phase angle shifts v to the right of the current i. Consequently i leads v for a series RC circuit. The
phase angle is constrained to the range 08 908. For ð1=!CÞ R, the angle ¼ 08, and for ð1=!CÞ R, the
angle ¼ 908. See Fig. 9-4.

Fig. 9-4